题目内容
当n=分析：对y=（m+n）xn+（m-n）x的图象是抛物线的判定，需满足n=2，又其顶点在原点，需满足m-n=0，则m、n的值即可求出，根据解得的函数解析式判断抛物线的开口方向．
解答：解：若函数y=（m+n）xn+（m-n）x的图象满足是抛物线，且其顶点在原点，
则
，解得，
，
故函数y=4x2，又由于a=4＞0，则抛物线的开口向上．
则
|
|
故函数y=4x2，又由于a=4＞0，则抛物线的开口向上．
点评：本题考查了二次函数的性质，需掌握抛物线函数需满足的条件及开口方向的判定．
练习册系列答案
相关题目
11、一列长为120米的火车匀速行驶，经过一条长为160米的隧道，从车头驶入隧道入口到车尾离开隧道出口公用14秒，设车头驶入隧道入口x秒时，火车在隧道内的长度为y米．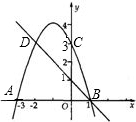
如图，已知抛物线y=ax2+bx+3的图象与x轴交于A、B两点，与y轴交于点C，且点C、D是抛物线上的一对对称点．