题目内容
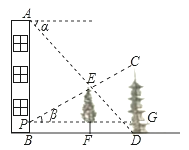
【题目】如图,在楼房AB和塔CD之间有一棵树EF,从楼顶A处经过树顶E点恰好看到塔的底部D点,且俯角α为45°.从距离楼底B点1米的P点处经过树顶E点恰好看到塔的顶部C点,且仰角β为30°.已知树高EF=6米,求塔CD的高度.(结果保留根号)
【答案】(1)△ACC1是等腰直角三角形(2)C2 (1,-4)(3)先将△AB1C1向右平移4个单位,然后再向下平移4个单位
【解析】试题分析:根据题意求出∠BAD=∠ADB=45°,进而根据等腰直角三角形的性质求得FD,在Rt△PEH中,利用特殊角的三角函数值分别求出BF,即可求得PG,在Rt△PCG中,继而可求出CG的长度.
试题解析:如图,

由题意可知∠BAD=∠ADB=45°,
∴FD=EF=6米,
在Rt△PEH中,∵tanβ=![]() ,
,
∴BF=![]() ,
,
∴PG=BD=BF+FD=5![]() +6,
+6,
在Rt△PCG中,∵tanβ=![]() ,
,
∴CG=(5![]() +6)
+6)![]() =5+2
=5+2![]() ,
,
∴CD=(6+2![]() )米.
)米.

练习册系列答案
相关题目
【题目】某市3月份某一周每天的最高气温统计如表,则这组数据(最高气温)的众数与中位数分别是( )
最高气温(℃) | 13 | 14 | 15 | 16 |
天数 | 1 | 3 | 1 | 2 |
A. 14℃,14℃B. 14℃,15℃C. 16℃,14℃D. 16℃,15℃
【题目】甲、乙、丙、丁四位备战南京青奥会射击选手在一次训练比赛中,这四位选手各射击10次,每人的平均成绩都是9.5环,方差如下表:
选手 | 甲 | 乙 | 丙 | 丁 |
方差(环2) | 0.35 | 0.018 | 0.22 | 0.055 |
则在这次训练比赛中,这四位选手发挥最稳定的是( )
A. 甲 B. 乙 C. 丙 D. 丁