题目内容
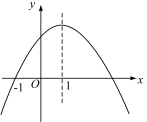
【题目】如图,已知二次函数y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,图象经过B(﹣3,0)、C(0,3)两点,且与x轴交于点A.
(1)求二次函数y=ax2+bx+c(a≠0)的表达式;
(2)在抛物线的对称轴上找一点M,使△ACM周长最短,求出点M的坐标;
(3)若点P为抛物线对称轴上的一个动点,直接写出使△BPC为直角三角形时点P的坐标.
【答案】(1)y=﹣x2﹣2x+3;(2)当点M的坐标为(﹣1,2)时,△ACM周长最短;(3)使△BPC为直角三角形时点P的坐标为(﹣1,﹣2),(﹣1,![]() ),(﹣1,
),(﹣1,![]() )或(﹣1,4).
)或(﹣1,4).
【解析】
(1)由抛物线的对称轴及点B的坐标可求出点A的坐标,由点A,B,C的坐标,利用待定系数法即可求出二次函数的表达式;
(2)连接BC,交直线x=-1于点M,此时△ACM周长最短,由点B,C的坐标,利用待定系数法可求出直线BC的函数表达式,再利用一次函数图象上点的坐标特征即可求出点M的坐标;
(3)设点P的坐标为(-1,m),结合点B,C的坐标可得出PB2,PC2,BC2的值,分∠BCP=90°,∠CBP=90°,∠BPC=90°三种情况考虑,①当∠BCP=90°时,利用勾股定理可得出关于m的一元一次方程,解之可得出m的值,进而可得出点P的坐标;②当∠CBP=90°时,利用勾股定理可得出关于m的一元一次方程,解之可得出m的值,进而可得出点P的坐标;③当∠BPC=90°时,利用勾股定理可得出关于m的一元二次方程,解之可得出m的值,进而可得出点P的坐标.综上,此题得解.
(1)∵二次函数y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,点B的坐标为(﹣3,0),
∴点A的坐标为(1,0).
将A(1,0),B(﹣3,0),C(0,3)代入y=ax2+bx+c,
得: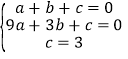 ,
,
解得: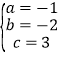 ,
,
∴二次函数的表达式为y=﹣x2﹣2x+3.
(2)连接BC,交直线x=﹣1于点M,如图1所示.
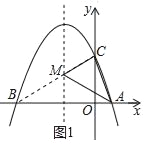
∵点A,B关于直线x=﹣1对称,
∴AM=BM.
∵点B,C,M三点共线,
∴此时AM+CM取最小值,最小值为BC.
设直线BC的函数表达式为y=kx+d(k≠0),
将B(﹣3,0),C(0,3)代入y=kx+d,
得:![]() ,
,
解得:![]() ,
,
∴直线BC的函数表达式为y=x+3.
当x=﹣1时,y=x+3=2,
∴当点M的坐标为(﹣1,2)时,△ACM周长最短.
(3)设点P的坐标为(﹣1,m),
∵点B的坐标为(﹣3,0),点C的坐标为(0,3),
∴PB2=[﹣3﹣(﹣1)]2+(0﹣m)2=m2+4,
PC2=[0﹣(﹣1)]2+(3﹣m)2=m2﹣6m+10,
BC2=[0﹣(﹣3)]2+(3﹣0)2=18.
分三种情况考虑(如图2):
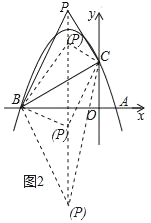
①当∠BCP=90°时,BC2+PC2=PB2,
∴18+m2﹣6m+10=m2+4,
解得:m=4,
∴点P的坐标为(﹣1,4);
②当∠CBP=90°时,BC2+PB2=PC2,
∴18+m2+4=m2﹣6m+10,
解得:m=﹣2,
∴点P的坐标为(﹣1,﹣2);
③当∠BPC=90°时,PB2+PC2=BC2,
∴m2+4+m2﹣6m+10=18,
整理得:m2﹣3m﹣2=0,
解得:m1=![]() ,m2=
,m2=![]() ,
,
∴点P的坐标为(﹣1,![]() )或(﹣1,
)或(﹣1,![]() ).
).
综上所述:使△BPC为直角三角形时点P的坐标为(﹣1,﹣2),(﹣1,![]() ),(﹣1,
),(﹣1,![]() )或(﹣1,4).
)或(﹣1,4).