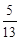题目内容
如图,在△ABC中,∠C=90°,D是BC边上一点,DE⊥AB于E,∠ADC=45°,若DE∶BE=1∶5,BE=3,求△ABD的面积。

13
分析:由已知条件可以证明△BED∽△BCA,然后根据其对应边成比例可将DE的长求出来,进而可求出AB的长,根据三角形的面积公式可求出结果.
解:在△AED中,∵DE⊥AB于E,
又∵DE:AE=1;5,
∴设DE=x,则AE=5x,
由勾股定理,AD2=AE2+ED2=(5x)2+x2=26x2,
∴AD=
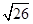 x.
x.在△ADC中,∵∠C=90°,∠ADC=45°,
∴∠DAC=45°.
由勾股定理,AC2+DC2=AD2=26x2,
∴AC=DC=
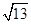 x.
x.在Rt△BED中,∵ED=x,BE=3,
由勾股定BD2=ED2+BE2=x2+32=x2+9,
∴BD=
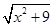 .
.在Rt△BED和Rt△BCA中,
∵∠B是公共角,
∠BED=∠BCA=90°,
∴△BED∽△BCA,而AB=3+5x.
∴
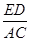 =
=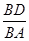 .
.即
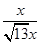 =
=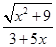 .
.解关于x的方程3+5x=
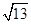 ?
?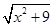 ,
,两边平方得:(3+5x)2=13?(x2+9),
化简得:2x2+5x-18=0,
即(x-1)(2x+9)=0,
∴x1="2" x2=-
 .
.∵x=ED>0,
∴x=ED=2,AE=5x=10.
∴AB=AE+BE=10+3=13.
∴S△ABD=
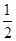 ED?AB=
ED?AB=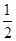 ×2×13=13.
×2×13=13.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
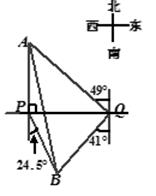
 , tan∠BCE=
, tan∠BCE= ,那么CE=
,那么CE= 
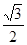 ,则α= 。
,则α= 。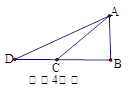
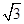 cm,则AB与平面P的夹角为
cm,则AB与平面P的夹角为 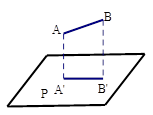
 中,
中, 则
则 的值为
的值为