题目内容
如图所示，一张边长为16cm的正方形硬纸板，把它的四个角都剪去一个边长为x cm的小正方形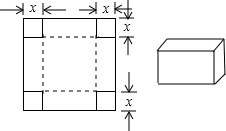
，然后把它折成一个无盖的长方体，设长方体的容积为V cm3，请回答下列问题：（1）用含有x的代数式表示V，则V=
（2）完成下表：
| x（cm） | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| V（cm2） |
分析：（1）由已知图形，折成的无盖的长方体的底是边长为16-2x（cm）的正方形，其高是xcm，则根据长方体的体积公式，表示出V．
（2）根据（1）得出的代数式，分别把x的值代入即可求出V．
（3）比较V值，易得结论．
（2）根据（1）得出的代数式，分别把x的值代入即可求出V．
（3）比较V值，易得结论．
解答：解：（1）V=（16-2x）2•x=x（16-2x）2．
故答案为：x（16-2x）2．
（2）分别把x=1，2，3，4，5，6，7代入x（16-2x）2
得V=196，288，300，256，180，96，28．
（3）观察上表，可以发现容积V的值不是随着x的值的增大而增大的，
从表中可知，当x取整数3时，容积V最大．
故答案为：x（16-2x）2．
（2）分别把x=1，2，3，4，5，6，7代入x（16-2x）2
得V=196，288，300，256，180，96，28．
（3）观察上表，可以发现容积V的值不是随着x的值的增大而增大的，
从表中可知，当x取整数3时，容积V最大．
点评：此题考查了学生对列代数式、代数式求值的理解与掌握．解答此题的关键是通过观察先确定折成的无盖的长方体的底是边长和高．
练习册系列答案
相关题目
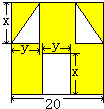“囧”（jiong）是近时期网络流行语，像一个人脸郁闷的神情．如图所示，一张边长为20的正方形的纸片，剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案（阴影部分）．
（1）“囧”（jiong）是近时期网络流行语，像一个人脸郁闷的神情．如图所示，一张边长为20的正方形的纸片，剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案（阴影部分）．设剪去的小长方形长和宽分别为x、y，剪去的两个小直角三角形的两直角边长也分别为x、y．