题目内容
 (2013•大庆)如图所示,在直角梯形ABCD中,AB为垂直于底边的腰,AD=1,BC=2,AB=3,点E为CD上异于C,D的一个动点,过点E作AB的垂线,垂足为F,△ADE,△AEB,△BCE的面积分别为S1,S2,S3.
(2013•大庆)如图所示,在直角梯形ABCD中,AB为垂直于底边的腰,AD=1,BC=2,AB=3,点E为CD上异于C,D的一个动点,过点E作AB的垂线,垂足为F,△ADE,△AEB,△BCE的面积分别为S1,S2,S3.(1)设AF=x,试用x表示S1与S3的乘积S1S3,并求S1S3的最大值;
(2)设
| AF | FB |
(3)在(2)的条件下,当t为何值时,S22=4S1S3.
分析:(1)直接根据三角形的面积公式解答即可;
(2)作DM⊥BC,垂足为M,DM与EF交与点N,根据
=t,可知AF=tFB,再由BM=MC=AD=1可得出
=
=
=
=
,所以NE=
,根据EF=FN+NE即可得出结论;
(3)根据AB=AF+FB=(t+1)FB=3,可得出FB=
,故可得出AF=tFB=
,根据三角形的面积公式可用t表示出S1,S3,S2,由s22=4S1S3.即可得出t的值.
(2)作DM⊥BC,垂足为M,DM与EF交与点N,根据
| AF |
| FB |
| NE |
| MC |
| DN |
| DM |
| AF |
| AF+FB |
| tFB |
| tFB+FB |
| t |
| t+1 |
| t |
| t+1 |
(3)根据AB=AF+FB=(t+1)FB=3,可得出FB=
| 3 |
| t+1 |
| 3t |
| t+1 |
解答: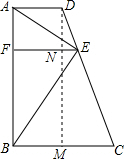 解:(1)∵S1=
解:(1)∵S1=
AD•AF=
x,
S3=
BC•BF=
×2×(3-x)=3-x,
∴S1S3=
x(3-x)
=
(-x2+3x)
=
[-(x-
)2+
]
=-
(x-
)2+
(0<x<3),
∴当x=
时,S1S3的最大值为
;
(2)作DM⊥BC,垂足为M,DM与EF交与点N,
∵
=t,
∴AF=tFB,
∵BM=MC=AD=1,
∴
=
=
=
=
,
∴NE=
,
∴EF=FN+NE=1+
=
;
(3)∵AB=AF+FB=(t+1)FB=3,
∴FB=
,
∴AF=tFB=
,
∴S1=
AD•AF=
×
=
,
S3=
BC•FB=
×2×
=
;
S2=
AB•FE=
×3×
=
,
∴S1S3=
,S22=
,
∴
=4×
,即4t2-4t+1=0,解得t=
.
 解:(1)∵S1=
解:(1)∵S1=| 1 |
| 2 |
| 1 |
| 2 |
S3=
| 1 |
| 2 |
| 1 |
| 2 |
∴S1S3=
| 1 |
| 2 |
=
| 1 |
| 2 |
=
| 1 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
=-
| 1 |
| 2 |
| 3 |
| 2 |
| 9 |
| 8 |
∴当x=
| 3 |
| 2 |
| 9 |
| 8 |
(2)作DM⊥BC,垂足为M,DM与EF交与点N,
∵
| AF |
| FB |
∴AF=tFB,
∵BM=MC=AD=1,
∴
| NE |
| MC |
| DN |
| DM |
| AF |
| AF+FB |
| tFB |
| tFB+FB |
| t |
| t+1 |
∴NE=
| t |
| t+1 |
∴EF=FN+NE=1+
| t |
| t+1 |
| 2t+1 |
| t+1 |
(3)∵AB=AF+FB=(t+1)FB=3,
∴FB=
| 3 |
| t+1 |
∴AF=tFB=
| 3t |
| t+1 |
∴S1=
| 1 |
| 2 |
| 1 |
| 2 |
| 3t |
| t+1 |
| 3t |
| 2(t+1) |
S3=
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| t+1 |
| 3 |
| t+1 |
S2=
| 1 |
| 2 |
| 1 |
| 2 |
| 2t+1 |
| t+1 |
| 3(2t+1) |
| 2(t+1) |
∴S1S3=
| 9t |
| 2(t+1)2 |
| 9(2t+1)2 |
| 4(t+1)2 |
∴
| 9(2t+1)2 |
| 4(t+1)2 |
| 9t |
| 2(t+1)2 |
| 1 |
| 2 |
点评:本题考查的是相似形综合题,熟知三角形的面积公式、二次函数的最值问题等相关知识是解答此题的关键.

练习册系列答案
相关题目
 (2013•大庆)如图,已知一次函数y=k1x+b(k1≠0)的图象分别与x轴,y轴交于A,B两点,且与反比例函数y=
(2013•大庆)如图,已知一次函数y=k1x+b(k1≠0)的图象分别与x轴,y轴交于A,B两点,且与反比例函数y= (2013•大庆)如图,三角形ABC是边长为1的正三角形,
(2013•大庆)如图,三角形ABC是边长为1的正三角形,
 (2013•大庆)如图,把一个直角三角形ACB(∠ACB=90°)绕着顶点B顺时针旋转60°,使得点C旋转到AB边上的一点D,点A旋转到点E的位置.F,G分别是BD,BE上的点,BF=BG,延长CF与DG交于点H.
(2013•大庆)如图,把一个直角三角形ACB(∠ACB=90°)绕着顶点B顺时针旋转60°,使得点C旋转到AB边上的一点D,点A旋转到点E的位置.F,G分别是BD,BE上的点,BF=BG,延长CF与DG交于点H. (2013•大庆)如图,平面直角坐标系中,以点C(2,
(2013•大庆)如图,平面直角坐标系中,以点C(2, (2013•大庆)如图所示,AB是半圆O的直径,AB=8,以AB为一直角边的直角三角形ABC中,∠CAB=30°,AC与半圆交于点D,过点D作BC的垂线DE,垂足为E.
(2013•大庆)如图所示,AB是半圆O的直径,AB=8,以AB为一直角边的直角三角形ABC中,∠CAB=30°,AC与半圆交于点D,过点D作BC的垂线DE,垂足为E.