题目内容
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4)

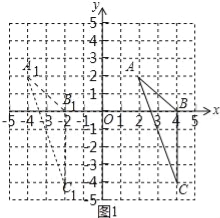
(1)请画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的![]() ,得到△A2B2C2,请在y轴右侧画出△A2B2C2,并求出∠A2C2B2的正弦值.
,得到△A2B2C2,请在y轴右侧画出△A2B2C2,并求出∠A2C2B2的正弦值.
【答案】(1)答案见解析;(2)![]()
【解析】
试题分析:(1)将A、B、C三点分别向左平移6个单位即可得到的△A1B1C1;(2)连接OA、OC,分别取OA、OB、OC的中点即可画出△A2B2C2,求出直线AC与OB的交点,求出∠ACB的正弦值即可解决问题.
试题解析:(1)如图1所示,
(2)如图2所示,
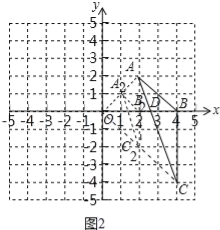
∵A(2,2),C(4,﹣4),B(4,0), ∴直线AC解析式为y=﹣3x+8,与x轴交于点D(![]() ,0),
,0),
∵∠CBD=90°, ∴CD=![]() =
=![]()
![]() ,∴sin∠DCB=
,∴sin∠DCB=![]() =
=![]() =
=![]() .
.
∵∠A2C2B2=∠ACB, ∴sin∠A2C2B2=sin∠DCB=![]() .
.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目