题目内容
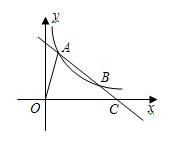 如图,O为坐标原点,点A(1,5)和点B(m,1)均在反比例函数y=
如图,O为坐标原点,点A(1,5)和点B(m,1)均在反比例函数y=| k | x |
(1)求m,k的值;
(2)设直线AB与x轴交于点C,求△AOC的面积.
分析:(1)把两点坐标分别代入解析式求解;(2)求直线AB的解析式及C点坐标,易求△AOC的面积.
解答:解:(1)将A(1,5)和点B(m,1)代入y=
得:m=5,k=5;(3分)
(2)(解法一)作AE⊥x轴于E,BF⊥x轴于F,
则AE∥BF,从而△AEC∽△BFC;(2分)
=
?
=
?CF=1;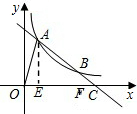
OC=OF+CF=6;(2分)
S△AOC=
OC×AE=
×6×5=15.(1分)
(解法二)设直AB所对应的一次函数关系式为:y=ax+b;(4分)
.?a=-1,b=6;
∴y=-x+6;(2分)
令y=0,得x=6,即OC=6,(1分)
S△AOC=
OC×AE=
×6×5=15.
| k |
| x |
(2)(解法一)作AE⊥x轴于E,BF⊥x轴于F,
则AE∥BF,从而△AEC∽△BFC;(2分)
| CF |
| CE |
| BF |
| AF |
| CF |
| CF+4 |
| 1 |
| 5 |

OC=OF+CF=6;(2分)
S△AOC=
| 1 |
| 2 |
| 1 |
| 2 |
(解法二)设直AB所对应的一次函数关系式为:y=ax+b;(4分)
|
∴y=-x+6;(2分)
令y=0,得x=6,即OC=6,(1分)
S△AOC=
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题可训练学生从多角度考虑问题,开阔视野.是一道很不错的题.

练习册系列答案
相关题目
 已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为( )
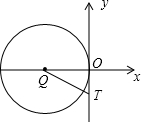
已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是腰长为5的等腰三角形时,则P点的坐标为( ) (2012•集美区一模)如图,O为坐标原点,小明在运动场练习踢足球,足球在点O处飞出,落在点B处,已知足球经过的路线是抛物线
(2012•集美区一模)如图,O为坐标原点,小明在运动场练习踢足球,足球在点O处飞出,落在点B处,已知足球经过的路线是抛物线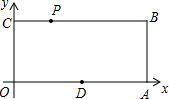 已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上以每秒1个单位的速度由C向B运动.
已知:如图,O为坐标原点,四边形OABC为矩形,A(10,0),C(0,4),点D是OA的中点,点P在BC上以每秒1个单位的速度由C向B运动. 如图:0为坐标原点,点A(1,4)和点B(a,1)均在反比例函数
如图:0为坐标原点,点A(1,4)和点B(a,1)均在反比例函数