题目内容
已知：如图，O为坐标原点，四边形OABC为矩形，A（10，0），C（0，4），点D是OA的中点，点P在BC上运动，当△ODP是腰长为5的等腰三角形时，则P点的坐标为（ ）分析：根据当OP=OD时，以及当OD=PD时和当OP=PD时，分别进行讨论得出P点的坐标，再选择即可．
解答：解：过P作PM⊥OA于M．
（1）当OP=OD时，
OP=5，CO=4，
∴易得CP=3，
∴P（3，4）；
（2）当OD=PD时，
PD=DO=5，PM=4，
∴易得MD=3，从而CP=2或CP'=8，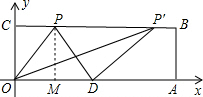
∴P（2，4）或（8，4）；
（3）当OP=PD时，易得CP=2.5，不合题意，舍去．
综上，满足题意的点P的坐标为（3，4）、（2，4）、（8，4），
故选D．
（1）当OP=OD时，
OP=5，CO=4，
∴易得CP=3，
∴P（3，4）；
（2）当OD=PD时，
PD=DO=5，PM=4，
∴易得MD=3，从而CP=2或CP'=8，
∴P（2，4）或（8，4）；
（3）当OP=PD时，易得CP=2.5，不合题意，舍去．
综上，满足题意的点P的坐标为（3，4）、（2，4）、（8，4），
故选D．
点评：此题主要考查了矩形的性质以及坐标与图形的性质和等腰三角形的性质，根据△ODP是腰长为5的等腰三角形进行分类讨论是解决问题的关键．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
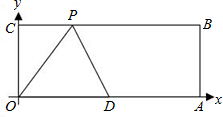
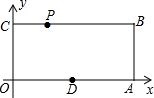已知，如图，O为坐标原点，四边形OABC为矩形，A（10，0），C（0，4），点D是OA的中点，点P在边BC上以每秒1个单位长的速度由点C向点B运动．
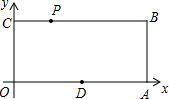已知：如图，O为坐标原点，四边形OABC为矩形，A（10，0），C（0，4），点D是OA的中点，点P在BC上以每秒1个单位的速度由C向B运动．