题目内容
在数学活动课上，小明提出这样一个问题：如图，∠B=∠C=90°，E是BC的中点，DE平分∠ADC，∠CED=35°，则∠EAB的度数是35°
35°
．分析：过点E作EF⊥AD于F，根据角平分线上的点到角的两边的距离相等可得CE=EF，再根据到角的两边距离相等的点在角的平分线上可得AE是∠BAD的平分线，然后求出=∠AEB，再根据直角三角形两锐角互余求解即可．
解答：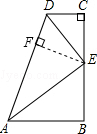
解：过点E作EF⊥AD于F，
∵DE平分∠ADC，
∴CE=EF，
∵E是BC的中点，
∴CE=BE，
∴BE=EF，
∴AE是∠BAD的平分线，
∵∠CED=35°，
∴∠AEB=90°-∠CED=90°-35°=55°，
∵∠B=90°，
∴∠EAB=90°-55°=35°．
故答案为：35°．
解：过点E作EF⊥AD于F，∵DE平分∠ADC，
∴CE=EF，
∵E是BC的中点，
∴CE=BE，
∴BE=EF，
∴AE是∠BAD的平分线，
∵∠CED=35°，
∴∠AEB=90°-∠CED=90°-35°=55°，
∵∠B=90°，
∴∠EAB=90°-55°=35°．
故答案为：35°．
点评：本题考查了角平分线上的点到角的两边的距离相等的性质，角平分线的判定，熟记性质并作辅助线是解题的关键．
练习册系列答案
相关题目
21、在数学活动课上，小明提出一个问题：“如图，在四边形ABCD中，∠B=∠C=90°，M是BC的中点，DM平分∠ADC，∠CMD=35°，则∠MAB是多少度”大家经过了一番热烈的讨论交流之后，小雨第一个得出了正确结论，你知道他说的是（ ）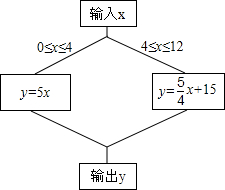
在数学活动课上，小明同学设计了一个计算程序，
在数学活动课上，小明提出这样一个问题：如图，∠B=∠C=90°，E是BC的中点，DE平分∠ADC，∠CED=35°，则∠EAB的度数是（ ）