题目内容
设实数a、b在数轴上对应的位置如图所示，化简
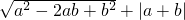的结果是________．
2b
分析：根据数轴得出a＜0＜b，|a|＜|b|，根据二次根式的性质和绝对值的意义化简即可．
解答：由数轴可知：a＜0＜b，|a|＜|b|，
∴原式=|a-b|+|a+b|=b-a+a+b=2b，
故答案为：2b．
点评：本题主要考查对二次根式的性质，绝对值的意义等知识点的理解和掌握，能正确去绝对值符号是解此题的关键．
分析：根据数轴得出a＜0＜b，|a|＜|b|，根据二次根式的性质和绝对值的意义化简即可．
解答：由数轴可知：a＜0＜b，|a|＜|b|，
∴原式=|a-b|+|a+b|=b-a+a+b=2b，
故答案为：2b．
点评：本题主要考查对二次根式的性质，绝对值的意义等知识点的理解和掌握，能正确去绝对值符号是解此题的关键．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
设实数a，b在数轴上对应的位置如图所示，化简| a2 |
| A、-2a+b | B、2a+b |
| C、-b | D、b |
设实数a、b在数轴上对应的位置如图所示，化简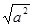
+|a+b|的结果是（ ）
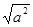+|a+b|的结果是（ ）
的结果是 ．