题目内容
【题目】已知:△ABC的中线BD、CE交于点O,F、G分别是OB、OC的中点. 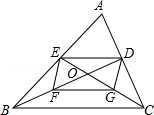
(1)求证:四边形DEFG是平行四边形;
(2)如果△ABC中AB=AC,四边形DEFG的形状是(直接写出结果).
【答案】
(1)证明:∵D、E分别为AC、AB的中点
∴ED∥BC,ED= ![]() BC.
BC.
同理FG∥BC,FG= ![]() BC,
BC,
∴ED∥FG,ED=FG,
∴四边形DEFG是平行四边形
(2)矩形
【解析】解:(2)如图1,当AB=AC时,DEFG变成矩形. 理由如下:
连接AO并延长交BC于点M.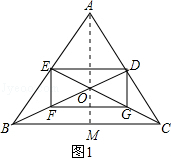
∵三角形的三条中线相交于同一点,△ABC的中线BD、CE交于点O,
∴M为BC的中点,
当AB=AC时,AM⊥BC,
∵E,F,G分别是AB,OB,OC的中点,
∴EF∥AO,FG∥BC,
∴EF⊥FG;
∴四边形EFGH是矩形.
所以答案是:矩形.
【考点精析】解答此题的关键在于理解等腰三角形的性质的相关知识,掌握等腰三角形的两个底角相等(简称:等边对等角),以及对三角形中位线定理的理解,了解连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目

