题目内容
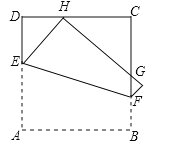
【题目】（2017湖南省长沙市，第12题，3分）如图，将正方形ABCD折叠，使顶点A与CD边上的一点H重合（H不与端点C，D重合），折痕交AD于点E，交BC于点F，边AB折叠后与边BC交于点G．设正方形ABCD的周长为m，△CHG的周长为n，则
的值为（ ）
A. 
B. 
C. 
D. 随H点位置的变化而变化
【答案】B
【解析】解：连接AH、AG，作AM⊥HG于M．
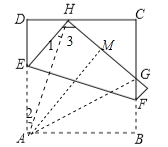
∵EA=EH，∴∠1=∠2．
∵∠EAB=∠EHG=90°，∴∠HAB=∠AHG．
∵DH∥AB，∴∠DHA=∠HAB=∠AHM．
∵AH=AH，∠D=∠AMH=90°，∴△AHD≌△AHM，∴DH=HM，AD=AM．
∵AM=AB，AG=AG，∴Rt△AGM≌Rt△AGB，∴GM=GB，
∴△GCH的周长=n=CH+HM+MG+CG=CH+DH+CG+GB=2BC．
∵四边形ABCD的周长=m=4BC，∴
．故选B．
金牌课堂练系列答案
三新快车金牌周周练系列答案
【题目】某校初三体育考试选择项目中，选择篮球项目和排球项目的学生比较多
为了解学生掌握篮球技巧和排球技巧的水平情况，进行了抽样调查，过程如下，请补充完整．
收集数据从选择篮球和排球的学生中各随机抽取16人，进行了体育测试，测试成绩
十分制
如下：
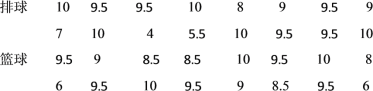
整理、描述数据按如下分数段整理、描述这两组样本数据：
|
|
|
| 10 | |
排球 | 1 | 1 | 2 | 7 | 5 |
篮球 |
说明：成绩
分及以上为优秀，6分及以上为合格，6分以下为不合格
分析数据两组样本数据的平均数、中位数、众数如下表所示：
项目 | 平均数 | 中位数 | 众数 |
排球 |
|
| 10 |
篮球 |
|
|
|
得出结论
如果全校有160人选择篮球项目，达到优秀的人数约为______人；
初二年级的小明和小军看到上面数据后，小明说：排球项目整体水平较高小军说：篮球项目整体水平较高．
你同意______的看法，理由为______
至少从两个不同的角度说明推断的合理性
