题目内容
【题目】如图,已知抛物线y=﹣x2+2x经过原点O,且与直线y=x﹣2交于B,C两点.
(1)求抛物线的顶点A的坐标及点B,C的坐标;
(2)求证:∠ABC=90°;
(3)在直线BC上方的抛物线上是否存在点P,使△PBC的面积最大?若存在,请求出点P的坐标;若不存在,请说明理由;
【答案】(1) A(1,1) ,B(2,0),C(﹣1,﹣3) (2)见解析 (3)(![]() ,
,![]() )
)
【解析】(1)把抛物线解析式化为顶点式可求得A点坐标,联立抛物线与直线的解析式可求得B、C的坐标;
(2)由A、B、C的坐标可求得AB2、BC2和AC2,由勾股定理的逆定理可判定△ABC是直角三角形;
(3)过点P作PG∥y轴,交直线BC于点G,设出P点坐标,则可表示出G点坐标,从而可表示出PG的长,则可表示出△PBC的面积,利用二次函数的性质可求得其最大值时P点坐标.
(1)∵y=-x2+2x=-(x-1)2+1,
∴抛物线顶点坐标A(1,1),
联立抛物线与直线解析式可得![]() ,解得
,解得![]() 或
或![]() ,
,
∴B(2,0),C(-1,-3);
(2)证明:
由(1)可知B(2,0),C(-1,-3),A(1,1),
∴AB2=(1-2)2+12=2,BC2=(-1-2)2+(-3)2=18,AC2=(-1-1)2+(-3-1)2=20,
∴AC2=AB2+BC2,
∴△ABC是直角三角形,
∴∠ABC=90°;
(3)如图,过点P作PG∥y轴,交直线BC于点G,
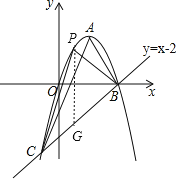
设P(t,-t2+2t),则G(t,t-2),
∵点P在直线BC上方,
∴PG=-t2+2t-(t-2)=-t2+t+2=-(t-![]() )2+
)2+![]() ,
,
∴S△PBC=S△PGB+S△PGC=![]() PG[2-(-1)]=
PG[2-(-1)]=![]() PG=-
PG=-![]() (t-
(t-![]() )2+
)2+![]() ,
,
∵-![]() <0,
<0,
∴当t=![]() 时,S△PBC有最大值,此时P点坐标为(
时,S△PBC有最大值,此时P点坐标为(![]() ,
,![]() ),
),
即存在满足条件的点P,其坐标为(![]() ,
,![]() )
)