题目内容
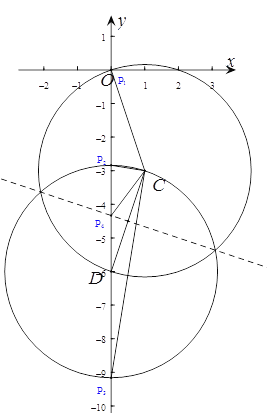
【题目】已知直线y=2x-5与x轴和y轴分别交于点A和点B,点C(1,n)在直线AB上,点D在y轴的负半轴上,且CD=![]() .
.
(1)求点C、点D的坐标.
(2)若P为y轴上的点,当△PCD为等腰三角形时,求点P的坐标.
(3)若点M为x轴上一动点(点M不与点O重合),N为直线y=2x-5上一动点,是否存在点M、N,使得△AMN与△AOB全等?若存在,求出点N的坐标;若不存在,请说明理由.


图1 图2
【答案】(1)C(1,-3),D(0,-6);(2)P(0, ![]() ) 、P(0,
) 、P(0, ![]() ) 、P(0,0)、P(0,
) 、P(0,0)、P(0, ![]() );(3)N(5,5)或N(
);(3)N(5,5)或N(![]() )或N(
)或N(![]() ).
).
【解析】试题分析:(1)先确定点C的坐标,设点D坐标为(0,d)(d<0),则有CD2=(1-0)2+(-3-d)2=![]() ,解之即可得;
,解之即可得;
(2)分别以点C、点D为圆心,CD为半径画圆,圆与y轴即为满足条件的点,作CD的中垂线与y轴的交点也满足条件,然后根据CD的长以及等腰三角形的性质即可得;
(3)分△AM1N1≌△AOB与△AM1N1≌△ABO两种情况,画出相应的图形进行求解即可得.
试题解析:(1)当x=1时,y=2x-5=-3,所以C(1,-3),
设点D坐标为(0,d)(d<0),则有CD2=(1-0)2+(-3-d)2=![]() ,解得:d=0(舍去)或d=-6,所以D(0,-6);
,解得:d=0(舍去)或d=-6,所以D(0,-6);
(2)当P1C=CD时,由(1)计算可知此时P1与原点O重合,所以P1(0,0),
当PC为底时,如图,此时PD=CD=![]() ,所以P2(0,-6-
,所以P2(0,-6-![]() )、P3(0,-6+
)、P3(0,-6+![]() ),
),
当CD为底边时,设P点坐标为(0,p),由题意则有(-3-p)2+12=(-6-p)2,解得:p=![]() ,所以P4(0,
,所以P4(0, ![]() ),
),
综上,点P坐标为: P1(0,0)、P2(0, ![]() ) 、P3(0,
) 、P3(0, ![]() )、P4(0,
)、P4(0, ![]() );
);
(3)由y=2x-5与x轴和y轴分别交于点A和点B可知OA=2.5,OB=5,AB=![]() ,
,
如图所示,当△AM1N1≌△AOB时,AM=AO,M1N1=OB,所以N1(5,5),
当△AM1N1≌△ABO时,AN3=AO=2.5,过点N3作N3E2⊥OA,
则有△AE2N3∽△AOB,∴![]() ,
,
即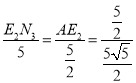 ,∴E2N3=
,∴E2N3=![]() ,AE2=
,AE2=![]() ,
,
同理E1N2=![]() ,AE1=
,AE1=![]() ,
,
∴N3(![]() ),N2(
),N2(![]() ),
),
综上,点N的坐标为:N1(5,5),N2(![]() ),N3(
),N3(![]() ).
).
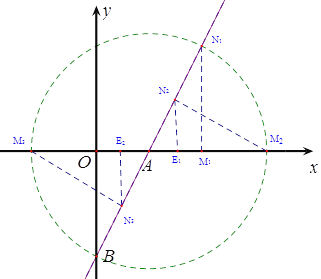

【题目】八(1)班同学为了解2015年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,
月均用水量 | 频数(户) | 频率 |
| 6 | 0.12 |
| m | 0.24 |
| 16 | 0.32 |
| 10 | 0.20 |
| 4 | n |
| 2 | 0.04 |
请解答以下问题:
(1)这里采用的调查方式是 (填“普查”或“抽样调查”),样本容量是 ;
(2)填空: ![]() ,
, ![]() ,并把频数分布直方图补充完整;
,并把频数分布直方图补充完整;
(3)若将月均用水量的频数绘成扇形统计图,则月均用水量“
(4)若该小区有1000户家庭,求该小区月均用水量超过10t的家庭大约有多少户?





