题目内容
等腰三角形的底边为7cm，一边上的中线把其周长分为两部分的差为3cm，则腰长为
- A.20cm
- B.10cm
- C.10cm或4cm
- D.4cm
C
分析：设腰长为xcm，根据中点的定义可求得AD与CD的长，因为没有指明哪部分大，故应该分两种情况进行分析，从而求解．
解答：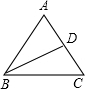
解：设腰长为xcm
如图，∵AC=xcm，点D是AC的中点
∴AD=CD=
xcm
①当AB+AD-（BC+CD）=3，即AB-BC=3，因为BC=7cm，所以AB=10cm；
②当BC+CD-（AB+AD）=3，即BC-AB=3，因为BC=7cm，所以AB=4cm；
故选C．
点评：此题主要考查等腰三角形的性质，注意分类讨论思想的运用．
分析：设腰长为xcm，根据中点的定义可求得AD与CD的长，因为没有指明哪部分大，故应该分两种情况进行分析，从而求解．
解答：
解：设腰长为xcm如图，∵AC=xcm，点D是AC的中点
∴AD=CD=
xcm①当AB+AD-（BC+CD）=3，即AB-BC=3，因为BC=7cm，所以AB=10cm；
②当BC+CD-（AB+AD）=3，即BC-AB=3，因为BC=7cm，所以AB=4cm；
故选C．
点评：此题主要考查等腰三角形的性质，注意分类讨论思想的运用．
练习册系列答案
第三学期赢在暑假系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案
相关题目
等腰三角形的底边为a，顶角是底角的4倍，则腰上的高是（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|