题目内容
已知，实数x，y，z满足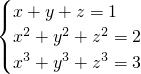
，则x4+y4+z4=
- A.4
- B.
- C.
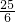
- D.以上都不对
C
分析：根据已知条件先求出xy+xz+yz=
，再求出xyz=，根据完全平方公式即可求解．
解答：∵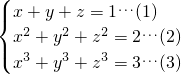
，
∴由（1）代入上式得：xy+xz+yz=（4），
而x3+y3+z3-3xyz=（x+y+z）（x2+y2+z2-xy-xz-yz），
把（3）（4）代入上式得：xyz=（5），
由（4）平方得：
；
把（5）代入上式得：
，
∴
．
故选C．
点评：本题考查了解高次方程，难度较大，关键是根据已知条件的正确变形．
分析：根据已知条件先求出xy+xz+yz=
，再求出xyz=，根据完全平方公式即可求解．解答：∵
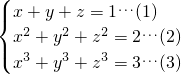，∴由（1）代入上式得：xy+xz+yz=
（4），而x3+y3+z3-3xyz=（x+y+z）（x2+y2+z2-xy-xz-yz），
把（3）（4）代入上式得：xyz=
（5），由（4）平方得：
；把（5）代入上式得：
，∴
．故选C．
点评：本题考查了解高次方程，难度较大，关键是根据已知条件的正确变形．
练习册系列答案
智趣暑假温故知新系列答案
英语小英雄天天默写系列答案
相关题目
已知，实数a，b在数轴上对应点的位置如图所示，化简