题目内容
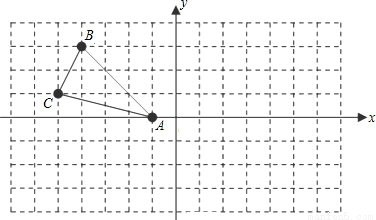
已知△ABC各顶点的直角坐标分别为A（3，4），B（0，0），C（c，0）．
（1）若c=5，求sinA的值；
（2）若∠A是钝角，求c的取值范围．
（1）若c=5，求sinA的值；
（2）若∠A是钝角，求c的取值范围．
分析：（1）由图知，AD=4，BD=3，CD=2，在Rt△ABD中，用勾股定理可求AB=5，同理，可求AC，那么在Rt△ACE中，sinA=
=
=
；
（2）先过A作AC′⊥AB交x轴于C′，设C′的坐标为（c，0），CE⊥AB，AC′⊥AB，那么有∠C′AB=∠ADB=90°，于是Rt△ABD∽Rt△C′BA，利用比例线段可求BC′，BC′=
，那么c＞
，∠BAC′为钝角．
| CE |
| AC |
| 4 | ||
2
|
2
| ||
| 5 |
（2）先过A作AC′⊥AB交x轴于C′，设C′的坐标为（c，0），CE⊥AB，AC′⊥AB，那么有∠C′AB=∠ADB=90°，于是Rt△ABD∽Rt△C′BA，利用比例线段可求BC′，BC′=
| 25 |
| 3 |
| 25 |
| 3 |
解答：
解：（1）根据已知作出示意图．
过点A作AD⊥x轴于D，过点C作CE⊥AB于E，则AD=4，BD=3，CD=2，
于是AB=5，AC=
=
=2
．
∵S△AOC=
AB•CE=
BC•AD，
∴CE=
=
=4．
因此sinA=
=
=
．
（2）过A作AC′⊥AB交x轴于C′，设C′的坐标为（c，0）．
∵AD⊥BC，AC′⊥AB，
∴∠C′AB=∠ADB=90°．
又∵∠B=∠B，
∴Rt△ABD∽Rt△C′BA．
∴
=
，
∴BC′=
=
=
．
故当∠A是钝角时，c的取值范围是c＞
．
解：（1）根据已知作出示意图．过点A作AD⊥x轴于D，过点C作CE⊥AB于E，则AD=4，BD=3，CD=2，
于是AB=5，AC=
| AD2+CD2 |
| 42+22 |
| 5 |
∵S△AOC=
| 1 |
| 2 |
| 1 |
| 2 |
∴CE=
| BC•AD |
| AB |
| 5×4 |
| 5 |
因此sinA=
| CE |
| AC |
| 4 | ||
2
|
2
| ||
| 5 |
（2）过A作AC′⊥AB交x轴于C′，设C′的坐标为（c，0）．
∵AD⊥BC，AC′⊥AB，
∴∠C′AB=∠ADB=90°．
又∵∠B=∠B，
∴Rt△ABD∽Rt△C′BA．
∴
| BC′ |
| AB |
| AB |
| BD |
∴BC′=
| AB2 |
| BD |
| 5×5 |
| 3 |
| 25 |
| 3 |
故当∠A是钝角时，c的取值范围是c＞
| 25 |
| 3 |
点评：本题利用了勾股定理、三角形面积公式，相似三角形的判定和性质．
练习册系列答案
相关题目
