题目内容
已知抛物线y=x2-3mx+m+n，要达到对所有的实数m，抛物线都与x轴有交点，n必须
- A.n≤-
- B.n≥
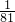
- C.n≤-
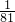
- D.n≤-1
A
分析：抛物线开口向上，要它对所有的实数m与x轴都有交点，则无论m取何值，△≥0．
解答：要使抛物线y=x2-3mx+m+n，要达到对所有的实数m，抛物线都与x轴有交点，即无论m取何值，
都有△=（-3m）2-4×1×（m+n）≥0成立，则
9m2-4m-4n=9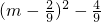
-4n≥0，
∴-
-4n≥0．
解可得：n≤-，
故选A．
点评：主要考查了二次函数的性质与一元二次方程之间的关系：与x轴有交点，那么根的判别式不小于0．
分析：抛物线开口向上，要它对所有的实数m与x轴都有交点，则无论m取何值，△≥0．
解答：要使抛物线y=x2-3mx+m+n，要达到对所有的实数m，抛物线都与x轴有交点，即无论m取何值，
都有△=（-3m）2-4×1×（m+n）≥0成立，则
9m2-4m-4n=9
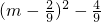-4n≥0，∴-
-4n≥0．解可得：n≤-
，故选A．
点评：主要考查了二次函数的性质与一元二次方程之间的关系：与x轴有交点，那么根的判别式不小于0．
练习册系列答案
相关题目
已知抛物线y=x2-8x+c的顶点在x轴上，则c等于（ ）
| A、4 | B、8 | C、-4 | D、16 |
（1）求b+c的值；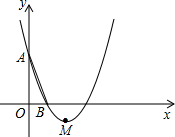
（2012•虹口区一模）如图，在平面直角坐标系xOy中，已知抛物线y=x2+bx+c经过A（0，3），B（1，0）两点，顶点为M．