题目内容
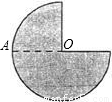
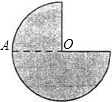如图，把半径为1的四分之三圆形纸片沿半径OA剪开，依次用得到的半圆形纸片和四分之一圆形纸片做成两个圆锥的侧面，则这两个圆锥的底面积之比为（ ）| A、5：1 | B、4：1 | C、3：1 | D、2：1 |
分析：可利用圆锥侧面展开图的弧长=底面周长得到圆锥底面半径，进而求得圆锥面积，比较即可．
解答：解：由题意知，小扇形的弧长为
，则它组成的圆锥的底面半径=
，小圆锥的底面面积=
；
大扇形的弧长为π，则它组成的圆锥的底面半径=
，大圆锥的底面面积=
，
∴大圆锥的底面面积：小圆锥的底面面积=4：1，故选B．
| π |
| 2 |
| 1 |
| 4 |
| π |
| 16 |
大扇形的弧长为π，则它组成的圆锥的底面半径=
| 1 |
| 2 |
| π |
| 4 |
∴大圆锥的底面面积：小圆锥的底面面积=4：1，故选B．
点评：本题利用了扇形面积公式，弧长公式，圆的周长公式求解．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
