题目内容
如图,矩形ABCD中,对角线AC、BD相交于点O,试问:是否存在一个圆,使A、B、C、D四个点都在这个圆上?如果存在,请指出这个圆的圆心和半径;如果不存在,说明理由.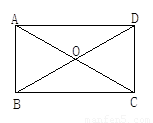
【答案】
存在,以O为圆心,OA为半径的圆.
【解析】
试题分析：根据矩形的性质可得OA=OB=OC=OD，再根据圆的基本概念即可得到结果.
∵矩形ABCD
∴OA=OB=OC=OD
∴存在一个以O为圆心,OA为半径的圆，使A、B、C、D四个点都在这个圆上.
考点：矩形的性质，圆的基本概念
点评：特殊四边形的性质的应用是初中数学平面图形中极为重要的知识点，与各个知识点结合极为容易，是中考中的热点，在各种题型中均有出现，需多加关注.
练习册系列答案
相关题目
14、如图矩形ABCD中BC=8，AB=4，将矩形纸片沿对角线对折，使C点落在F处，BC与AD边交于点E，则下列四个结论中：
如图矩形ABCD中，E为BC上一点，DF⊥AE于F．
29、如图矩形ABCD中，DP平分∠ADC交BC于P点，将一个直角三角板的直角顶点放在P点处，且使它的一条直角边过A点，另一条直角边交CD于E．找出图中与PA相等的线段．并说明理由．
如图矩形ABCD中，过A，B两点的⊙O切CD于E，交BC于F，AH⊥BE于H，连接EF．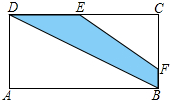
如图矩形ABCD中，AB=8cm，CB=4cm，E是DC的中点，BF=