Question

【题目】如图,在ABCD中,E是DC的中点,F是AE的中点,FC与BE交于G.求证:GF=GC.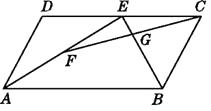

Answer 1

【答案】证明:如图,取BE的中点H,连接FH,CH.

∵F是AE的中点,H是BE的中点,
∴FH是△ABE的中位线.
∴FH∥AB且FH= AB.
在ABCD中,AB∥DC,AB=DC.
又∵点E是DC的中点,
∴EC= DC= AB.
∴FH=EC.
又∵AB∥DC,∴FH∥EC.
∴四边形EFHC是平行四边形.
∴GF=GC
【解析】抓住已知条件：E是DC的中点,F是AE的中点，因此取BE的中点H,连接FH,CH，就可证明FH是△ABE的中位线，得出FH∥AB且FH= AB，再根据平行四边形的性质及点E是DC的中点，证明FH=EC，EC∥FH，就可证明四边形EFHC是平行四边形然后根据平行四边形的对角线互相平分，就可证得结论。