题目内容
【题目】已知点A(a,0)、B(b,0),且![]() +|b﹣2|=0.
+|b﹣2|=0.

(1)求a、b的值.
(2)在y轴的正半轴上找一点C,使得三角形ABC的面积是15,求出点C的坐标.
(3)过(2)中的点C作直线MN∥x轴,在直线MN上是否存在点D,使得三角形ACD的面积是三角形ABC面积的![]() ?若存在,求出点D的坐标;若不存在,请说明理由.
?若存在,求出点D的坐标;若不存在,请说明理由.
【答案】(1)a=﹣4,b=2;(2)C(0,5);(3)D(3,5)或(﹣3,5).
【解析】试题分析:(1)根据非负数的性质列方程,解方程即可得到结论;
(2)由A(﹣4,0)、B(2,0),得到AB=6,根据三角形ABC的面积是15,列方程求解即可得到结论;
(3)根据三角形ABC的面积是15列方程,解方程即可得到结论.
试题解析:解:(1)∵(a+4)2+|b﹣2|=0,∴a+4=0,b﹣2=0,∴a=﹣4,b=2;
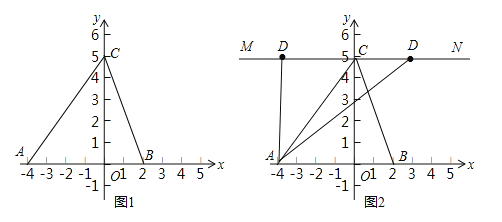
(2)如图1,∵A(﹣4,0)、B(2,0),∴AB=6,∵三角形ABC的面积是15,∴ ![]() ABOC=15,∴OC=5,∴C(0,5);
ABOC=15,∴OC=5,∴C(0,5);
(3)存在,如图2,∵三角形ABC的面积是15,∴S△ACD=![]() CDOC=
CDOC=![]() ×15,∴
×15,∴![]() CD×5=
CD×5=![]() ×15,∴CD=3,∴D(3,5)或(﹣3,5).
×15,∴CD=3,∴D(3,5)或(﹣3,5).

练习册系列答案
相关题目