题目内容
(本题满分10分)在平行四边形ABCD中,AB=10,∠ABC=60°,以AB为直径作⊙O,边CD切⊙O于点E.

1.⑴求圆心O到CD的距离;
2.⑵求DE的长;
3.⑶求由弧AE、线段AD、DE所围成的阴影部分的面积.
(结果保留π和根号)
1.(1)连接OE.∵CD切⊙O于点E,
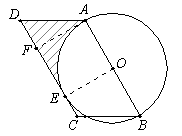
∴OE⊥CD.则OE的长度就是圆心O到CD的距离.
∵AB是⊙O的直径,OE是⊙O的半径,
∴OE=AB=5.即圆心⊙到CD的距离是5.
2.(2)过点A作AF⊥CD,垂足为F.∵四边形ABCD是平行四边形,∴∠B=∠D=60°,AB∥CD.∵AB∥CD,OE⊥CD,AF⊥CD,∴OA=OE=AF=EF=5.在Rt△ADF中,∠D=60°,AF=5,∴DF=,∴DE=5+.
3.(3)在直角梯形AOED中,OE=5,OA=5,DE=5+,
∴S梯形AOED=×(5+5+)×5=25+.∵∠AOE=90°,∴S扇形OAE=×π×52=π.∴S阴影= S梯形AOED- S扇形OAE=25+- π.即由弧AE、线段AD、DE所围成的阴影部分的面积为25+-π.
解析:略

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
 次后在函数 的图象上.(请填写相应的解析式)
次后在函数 的图象上.(请填写相应的解析式)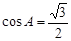 ,∠B的平分线BD交AC于D,BD=16.求AB的长.
,∠B的平分线BD交AC于D,BD=16.求AB的长.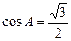 ,∠B的平分线BD交AC于D,BD=16.求AB的长.
,∠B的平分线BD交AC于D,BD=16.求AB的长. 在 ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.
在 ABCD中,AC、BD交于点O,过点O作直线EF、GH,分别交平行四边形的四条边于E、G、F、H四点,连结EG、GF、FH、HE.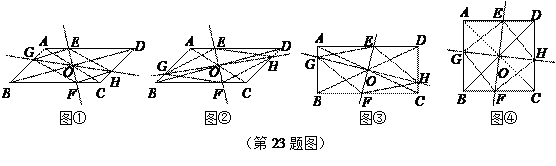
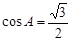 ,∠B的平分线BD交AC于D,BD=16.求AB的长.
,∠B的平分线BD交AC于D,BD=16.求AB的长.