题目内容
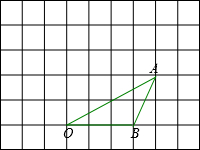如图，在每个小正方形的边长为1的方格纸中，将△OAB绕O点按逆时针方向旋转90°到△OA′B′．（1）画出△OA′B′（保留痕迹，不写画法）；
（2）求顶点A从开始到结束所经过的路径的长．（结果用含有π的式子表示）
分析：（1）找出点A、B绕点O逆时针旋转90°的对应点A′与B′的位置，然后顺次连接即可得到△OA′B′；
（2）先利用勾股定理求出AO的长度，再根据扇形的周长公式列式计算即可．
（2）先利用勾股定理求出AO的长度，再根据扇形的周长公式列式计算即可．
解答：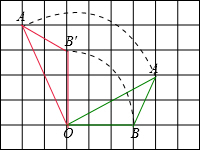
解：（1）如图所示；
（2）根据勾股定理得，OA=
=2
，
∴点A从开始到结束所经过的路径的长是：
=
=
．
解：（1）如图所示；（2）根据勾股定理得，OA=
| 42+22 |
| 5 |
∴点A从开始到结束所经过的路径的长是：
| 90π•OA |
| 360 |
90π•2
| ||
| 360 |
| ||
| 2 |
点评：本题考查了旋转变换与弧长的计算，找出旋转后对应点的位置是解题的关键．
练习册系列答案
相关题目
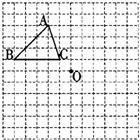15、如图，在每个小正方形的边长均为1个单位长度的方格纸中，有一个△ABC和一点O，△ABC的顶点和点O均与小正方形的顶点重合．
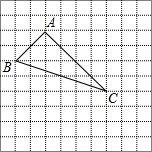如图．在每个小正方形的边长均为1个单位长度的方格纸中，有一个△ABC，△ABC的三个顶点均与小正方形的顶点重合．
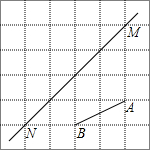（2013•哈尔滨）如图，在每个小正方形的边长均为1个单位长度的方格纸中，有线段AB和直线MN，点A，B，M，N均在小正方形的顶点上．
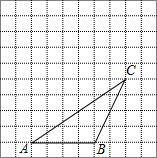如图，在每个小正方形边长为1的方格纸中，△ABC的顶点都在方格纸格点上．
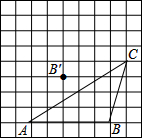如图，在每个小正方形边长为1的方格纸中，△ABC的顶点都在方格纸格点上．