题目内容
【题目】抛物线 y=x2+mx+n 过点(-1,8)和点(4,3)且与 x 轴交于 A,B 两点, 与 y 轴交于点 C
(1)求抛物线的解析式;
(2)如图1,AD 交抛物线于 D,交直线 BC 于点 G,且 AG=GD,求点 D 的坐标;
(3)如图2,过点 M(3,2)的直线交抛物线于 P,Q,AP 交 y 轴于点 E,AQ 交y 轴于点 F,求OE·OF的值.


【答案】(1)y=x2-4x+3;(2)D(![]() ,
,![]() )或(
)或(![]() ,
,![]() );(3)2.
);(3)2.
【解析】
(1)利用待定系数法求函数解析式即可;(2)先求得点A、B、C的坐标及直线BC的解析式,过点G作GR⊥x轴于点R,过点D作DK⊥x轴于点K(如图),由AG=GD,可得GR=![]() DK,设点D的坐标为(a,a2-4a+3),则点G的坐标为(
DK,设点D的坐标为(a,a2-4a+3),则点G的坐标为(![]() ,-
,-![]() +3),可得方程-
+3),可得方程-![]() +3=
+3=![]() (a2-4a+3),解方程求得a的值,即可得点D的坐标;(3)设AQ的解析式为y=ax-a,AP的解析式为y=bx-b,分别根抛物线的解析式联立,求得点P、Q的横坐标,在设PQ的解析式为y=kx+b,代入M(3,2)可得y=kx+2-3k. 将PQ的解析式为与抛物线解析式联立得到关于x的一元二次方程,然后依据一元二次方程根与系数的关系可求得ab=﹣2,再由ab的值可得到OEOF的值即可.
(a2-4a+3),解方程求得a的值,即可得点D的坐标;(3)设AQ的解析式为y=ax-a,AP的解析式为y=bx-b,分别根抛物线的解析式联立,求得点P、Q的横坐标,在设PQ的解析式为y=kx+b,代入M(3,2)可得y=kx+2-3k. 将PQ的解析式为与抛物线解析式联立得到关于x的一元二次方程,然后依据一元二次方程根与系数的关系可求得ab=﹣2,再由ab的值可得到OEOF的值即可.
(1)把点(-1,8)和点(4,3)代入y=x2+mx+n得,
![]() ,
,
解得![]() ,
,
∴y=x2-4x+3;
(2)令x2-4x+3=0,解得x=1或x=3,
∴A(1,0),B(3,0);
把x=0代入y=x2-4x+3得y=3,
∴C(0,3);
∴直线BC的解析式为y=-x+3.
如图,过点G作GR⊥x轴于点R,过点D作DK⊥x轴于点K,
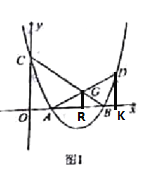
∴GR∥DK,
∵AG=GD,
∴GR=![]() DK,
DK,
设点D的坐标为(a,a2-4a+3),则点G的坐标为(![]() ,-
,-![]() +3),
+3),
即GR=-![]() +3,DK= a2-4a+3,
+3,DK= a2-4a+3,
∴-![]() +3=
+3=![]() (a2-4a+3),
(a2-4a+3),
整理得a2-3a-2=0,
解得,![]() ,
,![]() ,
,
∴D(![]() ,
,![]() )或(
)或(![]() ,
,![]() ).
).
(3)∵A(1,0),
设AQ的解析式为y=ax-a,AP的解析式为y=bx-b,
∴![]() ,解得x=1或x=a+3,
,解得x=1或x=a+3,
∴点Q的横坐标为a+3,
同理求得点P的横坐标为b+3.
设PQ的解析式为y=kx+b,把点 M(3,2)代入可得3k+b=2,即b=2-3k.
∴y=kx+2-3k.
∴kx+2-3k= x2-4x+3,即x2-(4+k)x+1+3k=0,
∵P、Q是抛物线y=x2-4x+3与直线PQ的交点,
∴a+3、b+3是方程x2-(4+k)x+1+3k=0的两个根,
∴a+3+b+3=4+k,(a+3)(b+3)=1+3k,
即a+b=k-2,ab+3(a+b)+9=1+3k,
∴ab+3(k-2)+9=1-3k,
整理得ab=-2,
∵OE=-b,OF=a,
∴OEOF=-ab=2.

 阅读快车系列答案
阅读快车系列答案



