题目内容
【题目】已知AB为⊙O的直径,OC⊥AB,弦DC与OB交于点F,在直线AB上有一点E,连接ED,且有ED=EF.
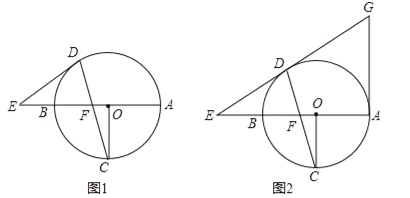
(1)如图1,求证:ED为⊙O的切线;
(2)如图2,直线ED与切线AG相交于G,且OF=1,⊙O的半径为3,求AG的长.
【答案】(1)证明见解析;(2)6.
【解析】
试题分析:(1)连接OD,由ED=EF可得出∠EDF=∠EFD,由对顶角相等可得出∠EDF=∠CFO;由OD=OC可得出∠ODF=∠OCF,结合OC⊥AB即可得知∠EDF+∠ODF=90°,即∠EDO=90°,由此证出ED为⊙O的切线;
(2)连接OD,过点D作DM⊥BA于点M,结合(1)的结论根据勾股定理可求出ED、EO的长度,结合∠DOE的正弦、余弦值可得出DM、MO的长度,根据切线的性质可知GA⊥EA,从而得出DM∥GA,根据相似三角形的判定定理即可得出△EDM∽△EGA,根据相似三角形的性质即可得出GA的长度.
试题解析:(1)证明:连接OD,如图1所示.

∵ED=EF,∴∠EDF=∠EFD,∵∠EFD=∠CFO,∴∠EDF=∠CFO.
∵OD=OC,∴∠ODF=∠OCF.
∵OC⊥AB,∴∠CFO+∠OCF=∠EDF+∠ODF=∠EDO=90°,∴ED为⊙O的切线.
(2)连接OD,过点D作DM⊥BA于点M,如图2所示.

由(1)可知△EDO为直角三角形,设ED=EF=a,EO=EF+FO=a+1,由勾股定理得:EO2=ED2+DO2,即(a+1)2=a2+32,解得:a=4,即ED=4,EO=5.
∵sin∠EOD=![]() ,cos∠EOD=
,cos∠EOD=![]() ,∴DM=ODsin∠EOD=3×
,∴DM=ODsin∠EOD=3×![]() =
=![]() ,MO=ODcos∠EOD=3×
,MO=ODcos∠EOD=3×![]() =
=![]() ,∴EM=EO﹣MO=5﹣
,∴EM=EO﹣MO=5﹣![]() =
=![]() ,EA=EO+OA=5+3=8.
,EA=EO+OA=5+3=8.
∵GA切⊙O于点A,∴GA⊥EA,∴DM∥GA,∴△EDM∽△EGA,∴![]() ,∴GA=
,∴GA=![]() =
=![]() =6.
=6.





