题目内容
如图，在等腰梯形ABCD中，AD∥BC，AB=CD=10，AD=6，BC=18，M是CD的中点，P是BC边上的一动点（P与B，C不重合），连接PM并延长交AD的延长线于Q．（1）当P在B，C之间运动到什么位置时，四边形ABPQ是平行四边形？请说明理由．
（2）当四边形ABPQ是直角梯形时，点P与C距离是多少？
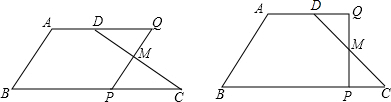
分析：（1）根据AAS证△CMP≌△DMQ，推出PC=DQ=6，求出BP、AQ，推出BP=AQ即可；
（2）作AE⊥BC于E，DF⊥BC于F，根据AAS证△ABE≌△DCF，推出BE=FC，证平行四边形AEFD，求出AE、BE的长，根据勾股定理求出PC即可．
（2）作AE⊥BC于E，DF⊥BC于F，根据AAS证△ABE≌△DCF，推出BE=FC，证平行四边形AEFD，求出AE、BE的长，根据勾股定理求出PC即可．
解答：（1）解：当CP=6时，四边形ABPQ是平行四边形．
理由：∵AD∥BC，
∴∠C=∠CDQ，∠QPC=∠Q，
∵CM=DM
∴△CMP≌△DMQ，
∴PC=DQ=6，
而BP=BC-PC=18-6=12，
AQ=AD+DQ=6+6=12，
∴BP=AQ，
∵AD∥BC，
∴四边形ABPQ是平行四边形．
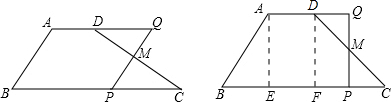
（2）解：作AE⊥BC于E，DF⊥BC于F，
由于AB=CD，∠B=∠C，∠AEB=∠DFC=90°，
∴△ABE≌△DCF，
∴BE=FC，
由于AE∥DF，AD∥EF，
∴四边形AEFD是平行四边形，
∴AD=EF，
∴BE=
=
=6，
∴AE=
=
=8，
由（1）知：QM=MP，
∴MP=4，
∴PC=
=
=3，
答：当四边形ABPQ是直角梯形时，点P与C距离是3．
理由：∵AD∥BC，
∴∠C=∠CDQ，∠QPC=∠Q，
∵CM=DM∴△CMP≌△DMQ，
∴PC=DQ=6，
而BP=BC-PC=18-6=12，
AQ=AD+DQ=6+6=12，
∴BP=AQ，
∵AD∥BC，
∴四边形ABPQ是平行四边形．
（2）解：作AE⊥BC于E，DF⊥BC于F，
由于AB=CD，∠B=∠C，∠AEB=∠DFC=90°，
∴△ABE≌△DCF，
∴BE=FC，
由于AE∥DF，AD∥EF，
∴四边形AEFD是平行四边形，
∴AD=EF，
∴BE=
| BC-AD |
| 2 |
| 18-6 |
| 2 |
∴AE=
| AB2-BE2 |
| 102-62 |
由（1）知：QM=MP，
∴MP=4，
∴PC=
| CM2-MP2 |
| 52-42 |
答：当四边形ABPQ是直角梯形时，点P与C距离是3．
点评：本题主要考查对勾股定理，平行四边形的性质和判定，全等三角形的性质和判定，平行线的性质，等腰梯形的性质等知识点的理解和掌握，能综合运用这些性质进行计算和推理是解此题的关键．
练习册系列答案
相关题目
在，求出这样的t的值；若不存在，请说明理由．
10、如图，在等腰梯形ABCD中，AD∥BC，AB=DC，E为AD的中点，求证：BE=CE．
已知：如图，在等腰梯形ABCD中，AD∥BC，AB=DC，点E、F分别在AB、DC上，且BE=3EA，CF=3FD．
（2012•广州）如图，在等腰梯形ABCD中，BC∥AD，AD=5，DC=4，DE∥AB交BC于点E，且EC=3，则梯形ABCD的周长是（ ）
