题目内容
 以下要求写出必要的演算步骤.
以下要求写出必要的演算步骤.
(1)(3xy2)•(-2xy)3;
(2)(c-2b+3a)(2b+c-3a);
(3)-2100×(0.5)99-(-1)99;
(4)先化简再求值:(x+y)(x2+y2)(x-y)(x4+y4),其中x=( )-1,y=-2;
)-1,y=-2;
(5)如图,AB∥CD,EF平分∠GFD,GF交AB于M,∠GMA=52°,求∠BEF的度数.
解:(1)原式=3xy2•(-8x3y3)=-24x4y5;
(2)原式=[c+(3a-2b)][c-(3a-2b)],
=c2-(3a-2b)2,
=c2-4b2+12ab-9a2;
(3)原式=-2×299×0.599-(-1),
=-2×(2×0.5)99+1,
=-2×1+1,
=-1;
(4)原式=[(x+y)(x-y)](x2+y2)(x4+y4),
=(x2-y2)(x2+y2)(x4+y4),
=(x4-y4)(x4+y4),
=x8-y8,
当x=( )-1=2,y=-2时,原式=28-(-2)8=0;
)-1=2,y=-2时,原式=28-(-2)8=0;
(5)∵AB∥CD,
∴∠BEF=180°-EFD,∠CFG=∠GMA=52°,
∴∠GFD=180°-∠CFG=128°
又∵EF平分∠GFD,∴∠EFD= ∠GFD=64°,
∠GFD=64°,
∴∠BEF=180°-∠EFD=116°.
分析:(1)先算乘方,再算乘法;
(2)式子满足平方差公式的结构,将其变形为(a+b)(a-b)的形式;
(3)将-2100×0.599变成-2×299×0.599,再反用积的乘方的运算性质;
(4)化简时,反复利用平方差公式.(5)由AB∥CD,利用同位角相等可求∠CFG的度数,再利用平角的定义可求∠DFG,再根据角平分线的定义求出∠EFD,再利用两直线平行同旁内角互补,从而求出∠BEF.
点评:本题考查了积的乘方,单项式的乘法,平方差公式,平行线的性质,熟练掌握运算法则和性质是解题的关键.
(2)原式=[c+(3a-2b)][c-(3a-2b)],
=c2-(3a-2b)2,
=c2-4b2+12ab-9a2;
(3)原式=-2×299×0.599-(-1),
=-2×(2×0.5)99+1,
=-2×1+1,
=-1;
(4)原式=[(x+y)(x-y)](x2+y2)(x4+y4),
=(x2-y2)(x2+y2)(x4+y4),
=(x4-y4)(x4+y4),
=x8-y8,
当x=(
 )-1=2,y=-2时,原式=28-(-2)8=0;
)-1=2,y=-2时,原式=28-(-2)8=0;(5)∵AB∥CD,
∴∠BEF=180°-EFD,∠CFG=∠GMA=52°,
∴∠GFD=180°-∠CFG=128°
又∵EF平分∠GFD,∴∠EFD=
 ∠GFD=64°,
∠GFD=64°,∴∠BEF=180°-∠EFD=116°.
分析:(1)先算乘方,再算乘法;
(2)式子满足平方差公式的结构,将其变形为(a+b)(a-b)的形式;
(3)将-2100×0.599变成-2×299×0.599,再反用积的乘方的运算性质;
(4)化简时,反复利用平方差公式.(5)由AB∥CD,利用同位角相等可求∠CFG的度数,再利用平角的定义可求∠DFG,再根据角平分线的定义求出∠EFD,再利用两直线平行同旁内角互补,从而求出∠BEF.
点评:本题考查了积的乘方,单项式的乘法,平方差公式,平行线的性质,熟练掌握运算法则和性质是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (-1,0),把△BOC向右平移2个单位长度后,一条直角边恰好在抛物线的对称轴上.
(-1,0),把△BOC向右平移2个单位长度后,一条直角边恰好在抛物线的对称轴上. 如图,已知在⊙O中,BD是弦,OB=6,AC是⊙O的直径,AC⊥BD于F,∠A=30°,则图中阴影部分的面积为________.
如图,已知在⊙O中,BD是弦,OB=6,AC是⊙O的直径,AC⊥BD于F,∠A=30°,则图中阴影部分的面积为________. 的解适合方程2x-5y=-1,那么m=________.
的解适合方程2x-5y=-1,那么m=________. 如图,四边形ABDC中,AD平分∠BAC,DB=DC,
如图,四边形ABDC中,AD平分∠BAC,DB=DC, 从正面看如图所示的正三棱柱,为
从正面看如图所示的正三棱柱,为



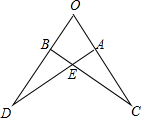 如图,点A、B分别在∠COD的边上,AD与BC相交于点E,若△OAD≌△OBC,且∠O=65°,∠C=20°,则∠OAD=________.
如图,点A、B分别在∠COD的边上,AD与BC相交于点E,若△OAD≌△OBC,且∠O=65°,∠C=20°,则∠OAD=________.