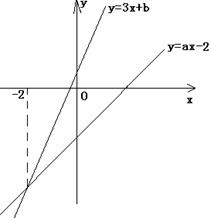
题目内容
 如图,已知直线l的解析式是y=
如图,已知直线l的解析式是y=| 4 |
| 3 |
| A、3秒或6秒 | B、6秒 |
| C、3秒 | D、6秒或16秒 |
分析:由y=
x-4可以求出与x轴、y轴的交点A(3,0)、B(0,-4)坐标,再根据勾股定理可得AB=5,当C在B上方,根据直线与圆相切时知道C到AB的距离等于1.5,然后利用三角函数可得到CB,最后即可得到C运动的距离和运动的时间;同理当C在B下方,利用题意的方法也可以求出C运动的距离和运动的时间.
| 4 |
| 3 |
解答: 解:如图,∵x=0时,y=-4,
解:如图,∵x=0时,y=-4,
y=0时,x=3,
∴A(3,0)、B(0,-4),
∴AB=5,
当C在B上方,直线与圆相切时,连接CD,
则C到AB的距离等于1.5,
∴CB=1.5÷sin∠ABC=1.5×
=2.5;
∴C运动的距离为:1.5+(4-2.5)=3,运动的时间为:3÷0.5=6;
同理当C在B下方,直线与圆相切时,
连接CD,则C运动的距离为:1.5+(4+2.5)=8,运动的时间为:8÷0.5=16.
故选D.
 解:如图,∵x=0时,y=-4,
解:如图,∵x=0时,y=-4,y=0时,x=3,
∴A(3,0)、B(0,-4),
∴AB=5,
当C在B上方,直线与圆相切时,连接CD,
则C到AB的距离等于1.5,
∴CB=1.5÷sin∠ABC=1.5×
| 5 |
| 3 |
∴C运动的距离为:1.5+(4-2.5)=3,运动的时间为:3÷0.5=6;
同理当C在B下方,直线与圆相切时,
连接CD,则C运动的距离为:1.5+(4+2.5)=8,运动的时间为:8÷0.5=16.
故选D.
点评:此题首先注意分类讨论,利用了切线的性质和三角函数等知识解决问题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
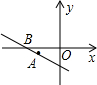 如图,已知直线y=kx+b经过A(-3,-1)和B(-4,0)两点,则不等式组
如图,已知直线y=kx+b经过A(-3,-1)和B(-4,0)两点,则不等式组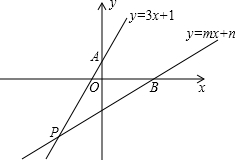 如图,已知直线l1:y=3x+1与y轴交于点A,且和直线l2:y=mx+n交于点P(-2,a),根据以上信息解答下列问题:
如图,已知直线l1:y=3x+1与y轴交于点A,且和直线l2:y=mx+n交于点P(-2,a),根据以上信息解答下列问题: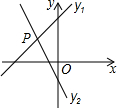 (2013•锦州模拟)如图,已知直线y1=x+m与y2=kx-1相交于点P(-1,1),则关于x的不等式x+m>kx-1的解集为
(2013•锦州模拟)如图,已知直线y1=x+m与y2=kx-1相交于点P(-1,1),则关于x的不等式x+m>kx-1的解集为