Question

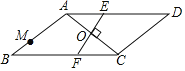
【题目】如图，在ABCD中，∠B=30°，AB=AC，O是两条对角线的交点，过点O作AC的垂线分别交边AD，BC于点E，F；点M是边AB的一个三等分点，则△AOE与△BMF的面积比为______．

Answer 1

【答案】或

【解析】

设AB=AC=m，根据平行四边形的性质可得OA=OC=AC=m，继而根据已知解三角形求得FC=m，通过证明△AOE≌△COF，求得AE=FC=m，从而求得S△AOE=m2，作AN⊥BC于N，求得BC=m，继而求得BF=BC﹣FC=m﹣m=m，然后作MH⊥BC于H，分点M为靠近点B的三等分点和靠近点A的三等分点两种情况求出S△BMF的值即可求得答案.

设AB=AC=m，

∵O是两条对角线的交点，∴OA=OC=AC=m，

∵∠B=30°，AB=AC，∴∠ACB=∠B=30°，

∵EF⊥AC，∴cos∠ACB= ，即cos30°=，∴FC=m，

∵AE∥FC，∴∠EAC=∠FCA，又∵∠AOE=∠COF，AO=CO，∴△AOE≌△COF，∴AE=FC=m，

∴OE=AE=m，∴S△AOE=OAOE=×m×m=m2，

作AN⊥BC于N，

∵AB=AC，∴BN=CN=BC，∵BN=AB=m，∴BC=m，

∴BF=BC﹣FC=m﹣m=m，

作MH⊥BC于H，如图1（点M为靠近点B的AB的三等分点），则BM=m，

∵∠B=30°，∴MH=BM=m，∴S△BMF=BFMH=×m×m=m2，

∴ ，

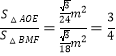如图2（点M为靠近点A的AB的三等分点），则BM=m，

∵∠B=30°，∴MH=BM=m，∴S△BMF=BFMH=×m×m=m2，

∴ ，

故答案为：或.