题目内容
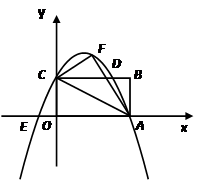
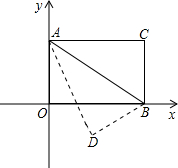
已知如图,矩形OABC的长OA=![]() ,宽OC=1,将△AOC沿AC翻折得△AFC.
,宽OC=1,将△AOC沿AC翻折得△AFC.
1.求过A、F、C三点的抛物线解析式;
2.设(1)中的抛物线与矩形OABC边CB相交于点D,与![]() 轴相交于另外一点E,若点M是
轴相交于另外一点E,若点M是![]() 轴上的点,N是
轴上的点,N是![]() 轴上的点,若以点E、M、D、N为顶点的四边形是平行四边形,试求点M、N的坐标
轴上的点,若以点E、M、D、N为顶点的四边形是平行四边形,试求点M、N的坐标
3.若动点P以每秒![]() 个单位长度的速度从C点出发沿CB 向终点B运动,同时动点Q从A点出发以每秒
个单位长度的速度从C点出发沿CB 向终点B运动,同时动点Q从A点出发以每秒![]() 个单位长度的速度沿射线AO运动,当P运动到B点时,P,Q同时停止运动.当点P运动时间t(秒)为何值时,以P、C、O为顶点的三角形与以Q、O、C为顶点的三角形相似?
个单位长度的速度沿射线AO运动,当P运动到B点时,P,Q同时停止运动.当点P运动时间t(秒)为何值时,以P、C、O为顶点的三角形与以Q、O、C为顶点的三角形相似?
1.![]()
2.M1(![]() ,0),N1(0,1);M2(
,0),N1(0,1);M2(![]() ,0),N2(0,1)
,0),N2(0,1)
3.t=![]() 或
或![]()
解析:(1)∵OA=![]() ,OC=1,∴tan∠OAC=
,OC=1,∴tan∠OAC=![]() .
.
∴∠OAC=30° ∠ACF=∠ACO=60°……………………1分
过P作PE⊥OA于E,交CB于G,则FG⊥CD.
∠GCF=30°, GF=![]() CF=
CF=![]() OC=
OC=![]() .
.
CF=![]() . ∴P(
. ∴P(![]() ,
,![]() )…………………………2分
)…………………………2分
设过 A、B、C三点抛物线解析式为![]() .∴c=1
.∴c=1
∴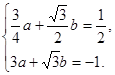 ……………………………………3分
……………………………………3分
解之,得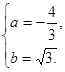 ∴
∴![]() .………………4分
.………………4分
(2)由![]() ,得
,得![]() =
=![]() ,
,![]() =
=![]() .
.
∴E(![]() ,0)……………………………………5分
,0)……………………………………5分
由![]() ,得
,得![]() =0,
=0, 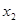 =
=![]() .∴D(
.∴D(![]() ,1).………………6分
,1).………………6分
①当DN∥EM且DN=EM时,当M在E点左侧时,M1(![]() ,0),此时N1(0,1)…7分
,0),此时N1(0,1)…7分
当M在E点右侧时,OM2=![]() .∴M2(
.∴M2(![]() ,0),此时N2(0,1)……8分
,0),此时N2(0,1)……8分
②当ED∥MN且ED=MN时,过D作DH⊥OA于H,M3(![]() ,0),N3(0,-1)……9分
,0),N3(0,-1)……9分
(3)若以P、C、Q为顶点的三角形与△QOC相似,因∠POC=∠QCO=90°,则有
CQ=OP或OC2=CQ·OP.
当P、Q在y轴同侧时:
由![]() ,得t=
,得t=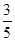 .………………………………10分
.………………………………10分
由![]() ,得
,得 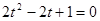 .
.
△=4-8=-4<0,故无解.
当P、Q在y轴异侧时:
由![]() ,得t=3>
,得t=3>![]() ,不合题意,舍去………………………11分
,不合题意,舍去………………………11分
由![]() ,得
,得 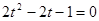 .
.
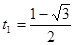 <0舍去,
<0舍去,![]() ∴t=
∴t=![]() 或
或![]() ……………………12分
……………………12分

 B=60°,以AB为轴对折后,使C点落在D点处,求D点坐标.
B=60°,以AB为轴对折后,使C点落在D点处,求D点坐标.


