题目内容
【题目】如图,已知抛物线L1:y=![]() x2-x-
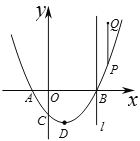
x2-x-![]() ,L1交x轴于A,B(点A在点B左边),交y轴于C,其顶点为D,P是L1上一个动点,过P沿y轴正方向作线段PQ∥y轴,使PQ=t,当P点在L1上运动时,Q随之运动形成的图形记为L2.
,L1交x轴于A,B(点A在点B左边),交y轴于C,其顶点为D,P是L1上一个动点,过P沿y轴正方向作线段PQ∥y轴,使PQ=t,当P点在L1上运动时,Q随之运动形成的图形记为L2.
(1)若t=3,求图形L2的函数解析式;
(2)过B作直线l∥y轴,若直线l和y轴及L1,L2所围成的图形面积为12,求t的值.
【答案】(1)y=![]() x2-x+
x2-x+![]() ;(2)4.
;(2)4.
【解析】
(1)Q点运动的图形,相当于抛物线向上平移t个单位,如下图:即:L2的图象为:y=![]() x2-x-
x2-x-![]() +t即可求解;
+t即可求解;
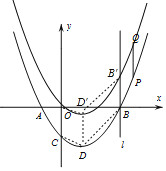
(2)直线l和y轴及L1,L2所围成的图形面积=平行四边形DD′B′B面积+平行四边形DD′CO的面积,即:S=D′D(xB-xC)即可求解.
y=![]() x2-x-
x2-x-![]() =
=![]() (x-1)2-2,
(x-1)2-2,
故:B(3,0),D(1,2)
(1)Q点运动的图形,相当于抛物线向上平移t个单位,如下图:
即:L2的图象为:y=![]() x2-x-
x2-x-![]() +t,
+t,
t=3,L2的函数解析式为:y=![]() x2-x+
x2-x+![]() ;
;
(2)L2的图象为:y=![]() x2-x-
x2-x-![]() +t,
+t,
直线l和y轴及L1,L2所围成的图形面积=平行四边形DD′B′B面积+平行四边形DD′CO的面积,
即:S=D′D(xB-xC)=t×3=12,
故t=4.

练习册系列答案
相关题目