题目内容
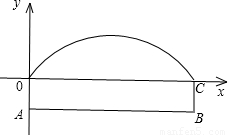
 如图所示,有一条双向公路隧道,其横断面由抛物线和矩形ABCO的三边组成,隧道的最大高度为4.9m,AB=10m,BC=2.4m,有一辆高为4m、宽为2m的汽车要通过此隧道,若不考虑其他因素,汽车离隧道石壁多少米时才不会碰到隧道顶部?(抛物线部分为隧道顶部,A0,BC为壁)
如图所示,有一条双向公路隧道,其横断面由抛物线和矩形ABCO的三边组成,隧道的最大高度为4.9m,AB=10m,BC=2.4m,有一辆高为4m、宽为2m的汽车要通过此隧道,若不考虑其他因素,汽车离隧道石壁多少米时才不会碰到隧道顶部?(抛物线部分为隧道顶部,A0,BC为壁)分析:根据题意得出抛物线的顶点坐标,设抛物线顶点式函数关系式为:y=a(x-5)2+2.5,求出函数解析式,然后求出当y=1.6时x的值,即可得出答案.
解答:解:由题意得,抛物线的顶点坐标为(5,2.5),且过(0,0)点,
设抛物线的解析式为:y=a(x-5)2+2.5,
当x=0时,y=0,则25a+2.5=0,
解得:a=-0.1,
故抛物线的解析式为:y=-0.1(x-5)2+2.5,
当y=4-2.4=1.6时,-0.1(x-5)2+2.5=1.6,
解得:x1=2,x2=8(不合题意舍去).
答:汽车离隧道石壁2米时才不会碰到隧道顶部.
设抛物线的解析式为:y=a(x-5)2+2.5,
当x=0时,y=0,则25a+2.5=0,
解得:a=-0.1,
故抛物线的解析式为:y=-0.1(x-5)2+2.5,
当y=4-2.4=1.6时,-0.1(x-5)2+2.5=1.6,
解得:x1=2,x2=8(不合题意舍去).
答:汽车离隧道石壁2米时才不会碰到隧道顶部.
点评:本题考查了二次函数的应用,解答本题的关键是将实际问题转化为数学模型,求出抛物线解析式,结合一元二次方程的知识解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
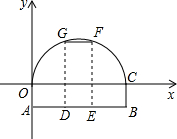
 如图所示,一条双向公路隧道,其横断面由抛物线和矩形ABCO的三边组成,隧道的最大高度为4.9m,AB=10m,BC=2.4m,现把隧道的横断面放在平面直角坐标系中.
如图所示,一条双向公路隧道,其横断面由抛物线和矩形ABCO的三边组成,隧道的最大高度为4.9m,AB=10m,BC=2.4m,现把隧道的横断面放在平面直角坐标系中.
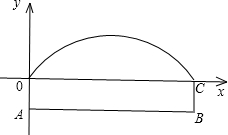
 如图所示,有一条双向公路隧道,其横断面由抛物线和矩形ABCO的三边组成,隧道的最大高度为4.9m,AB=10m,BC=2.4m,有一辆高为4m、宽为2m的汽车要通过此隧道,若不考虑其他因素,汽车离隧道石壁多少米时才不会碰到隧道顶部?(抛物线部分为隧道顶部,A0,BC为壁)
如图所示,有一条双向公路隧道,其横断面由抛物线和矩形ABCO的三边组成,隧道的最大高度为4.9m,AB=10m,BC=2.4m,有一辆高为4m、宽为2m的汽车要通过此隧道,若不考虑其他因素,汽车离隧道石壁多少米时才不会碰到隧道顶部?(抛物线部分为隧道顶部,A0,BC为壁)