题目内容
已知一次函数y1=2x-2k的图象与反比例函数y2=| k+3 | x |
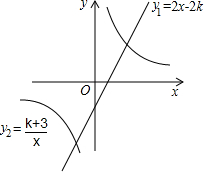 的纵坐标为-4.
的纵坐标为-4.(1)求两个函数的解析式;
(2)结合图象求出当y1<y2时,x的取值范围.
分析:(1)根据一次函数y1=2x-2k的图象与反比例函数y2=
的图象相交,其中一个交点的纵坐标为-4,得出关于m,k的二元一次方程组,即可得出函数解析式;
(2)根据解析式求出两函数交点坐标,即可得出当y1<y2时,x的取值范围.
| k+3 |
| x |
(2)根据解析式求出两函数交点坐标,即可得出当y1<y2时,x的取值范围.
解答:解:(1)由已知设交点A(m,-4),
则
,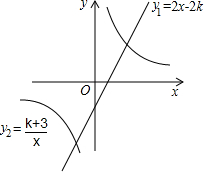
解得:
经检验:
是所列方程组的解,
∴y1=2x-2,
y2=
;
(2)由方程组
得2x2-2x-4=0,
∴x1=-1,x2=2,
由图象可知,当x<-1或0<x<2时y1<y2.
则
|
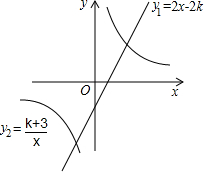
解得:
|
经检验:
|
∴y1=2x-2,
y2=
| 4 |
| x |
(2)由方程组
|
∴x1=-1,x2=2,
由图象可知,当x<-1或0<x<2时y1<y2.
点评:此题主要考查了反比例函数与一次函数交点坐标的性质,根据已知图象判定函数的大小关系是初中阶段的难点问题,同学们应重点掌握.

练习册系列答案
相关题目
 2,4)、(4,-2).
2,4)、(4,-2). (2012•德阳)已知一次函数y1=x+m的图象与反比例函数
(2012•德阳)已知一次函数y1=x+m的图象与反比例函数 已知一次函数y1=ax+b的图象与反比例函数y2=
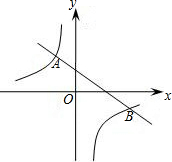
已知一次函数y1=ax+b的图象与反比例函数y2= 如图所示,已知一次函数y1=kx+b的图象经过A(1,2)、B(-1,0)两点,y2=mx+n的图象经过A、C(3,0)两点,则不等式组0<kx+b<mx+n的解集是( )
如图所示,已知一次函数y1=kx+b的图象经过A(1,2)、B(-1,0)两点,y2=mx+n的图象经过A、C(3,0)两点,则不等式组0<kx+b<mx+n的解集是( )