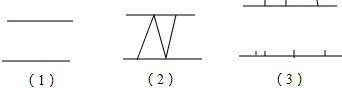题目内容
16、两条平行直线上各有n个点,用这n对点按如下的规则连接线段:
①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;
②符合①的要求的线段全部画出:
(连线情况不同时,三角形的总个数情况也不同)
(1)当n=1时,此时图中三角形的个数为0;
(2)当n=2时,此时图中三角形的个数为2;
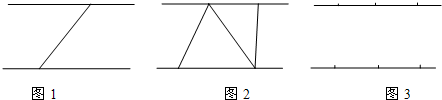
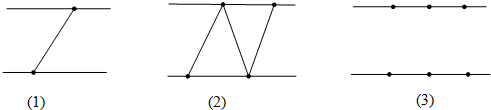
(3)当n=3时,如下图中线段连接不同,三角形的总个数有三种情况分别为:
(4)当n=4时,此时图中三角形的个数可能是
①平行线之间的点在连线段时,可以有共同的端点,但不能有其它交点;
②符合①的要求的线段全部画出:
(连线情况不同时,三角形的总个数情况也不同)
(1)当n=1时,此时图中三角形的个数为0;
(2)当n=2时,此时图中三角形的个数为2;
(3)当n=3时,如下图中线段连接不同,三角形的总个数有三种情况分别为:
4个或5个或6个
;
(4)当n=4时,此时图中三角形的个数可能是
6个或7个或8个或10个或12
个.分析:n=4时,分五种情况;当顺次连接各点时,即无三线共点时,有6个三角形;当有1组三线共点时,有7个三角形;当有2组三线共点时,有8个三角形;当有3组三线共点时,有10个三角形;当有4组三线共点时,有12个三角形.
解答:解:(3)4个或5个或6个;
(4)6个或7个或8个或10个或12.
(4)6个或7个或8个或10个或12.
点评:此题考查了平面图形的有规律变化,要求学生通过观察图形,分析、归纳并发现其中的规律,并应用规律解决问题.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目