题目内容
【题目】已知正方形ABCD的边长为4,一个以点A为顶点的45°角绕点A旋转,角的两边分别与边BC、DC的延长线交于点E、F,连接EF.设CE=a,CF=b.
(1)如图1,当∠EAF被对角线AC平分时,求a、b的值;
(2)当△AEF是直角三角形时,求a、b的值;
(3)如图3,探索∠EAF绕点A旋转的过程中a、b满足的关系式,并说明理由.
【答案】
(1)
解:∵四边形ABCD是正方形,
∴∠ACF=∠DCD=90°,
∵AC是正方形ABCD的对角线,
∴∠ACB=∠ACD=45°,
∴∠ACF=∠ACE,
∵∠EAF被对角线AC平分,
∴∠CAF=∠CAE,
在△ACF和△ACE中,
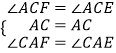 ,
,
∴△ACF≌△ACE,
∴CE=CE,
∵CE=a,CF=b,
∴a=b;
(2)
解:当△AEF是直角三角形时,
①当∠AEF=90°时,
∵∠EAF=45°,
∴∠AFE=45°,
∴△AEF是等腰直角三角形,
∴AF2=2FE2=2(CE2+CF2),
AF2=2(AD2+BE2),
∴2(CE2+CF2)=2(AD2+BE2),
∴CE2+CF2=AD2+BE2,
∴CE2+CF2=16+(4+CE)2,
∴CF2=8(CE+4)①
∵∠AEB+∠BEF=90°,∠AEB+∠BAE=90°,
∴∠BEF=∠BAE,
∴△ABE∽△ECF,
∴ ![]() ,
,
∴ ![]() ,
,
∴4CF=CE(CE+4)②,
联立①②得,CE=4,CF=8
∴a=4,b=8,
②当∠AFE=90°时,
同①的方法得,CF=4,CE=8,
∴a=8,b=4.
(3)
ab=32,
理由:如图,
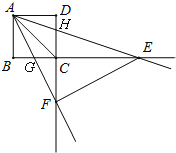
∵∠BAG+∠AGB=90°,∠AFC+∠CGF=90°,∠AGB=∠CGF,
∴∠BAG=∠AFC,
∵∠BAC=45°,
∴∠BAG+∠CAF=45°,
∴∠AFC+∠CAF=45°,
∵∠AFC+∠AEC=180°﹣(∠CFE+∠CEF)﹣∠EAF=180°﹣90°﹣45°=45°,
∴∠CAF=∠AEC,
∵∠ACF=∠ACE=135°,
∴△ACF∽△ECA,
∴ ![]() ,
,
∴EC×CF=AC2=2AB2=32
∴ab=32
【解析】(1)当∠EAF被对角线AC平分时,易证△ACF≌△ACE,因此CF=CE,即a=b.(2)分两种情况进行计算,①先用勾股定理得出CF2=8(CE+4)①,再用相似三角形得出4CF=CE(CE+4)②,两式联立解方程组即可;(3)先判断出∠AFC+∠CAF=45°,再判断出∠AFC+∠AEC=45°,从而求出∠AEC,而∠ACF=∠ACE=135°,得到△ACF∽△ECA,即可.此题是四边形综合题,主要考查了全等三角形的判定和性质,直角三角形的性质,相似三角形的性质和判定,解本题的关键是判断△ACF∽△ECA,也是本题的难点.





