题目内容
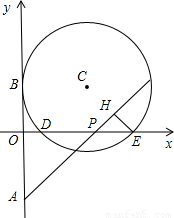
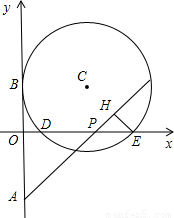
在坐标平面内,半径为R的⊙C与x轴交于点D(1,0)、E(5,0),与y轴的正半轴相切于点A。点A、B关于x轴对称,点P(a,0)在x的正半轴上运动,作直线BP,作EH⊥BP于H。

⑴求圆心C的坐标及半径R的值;
⑵△POB和△PHE随点P的运动而变化,若它们全等,求a的值;
⑶当a=6时,试确定直线BP与⊙C的位置关系并说明理由。
【答案】
(1)C(3,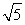 ),R=3;(2)a=2;(3)相离.
),R=3;(2)a=2;(3)相离.
【解析】
试题分析:(1)由题意知圆心C点的横坐标为DE中点的坐标,纵坐标和B点纵坐标相等,用切割线定理求出OB的长即可,C点的横坐标等于半径;
(2)因为△POA≌△PHE,OE的长为直角边和斜边的和,而OE的长已求,用OP表示PE,并且OA=OB.根据勾股定理求出OP的长即为a的值,过A作圆的切线为标准证明AP与⊙C的关系.
试题解析:(1)连接BC,则BC⊥y轴.取DE中点M,连CM,则CM⊥x轴.
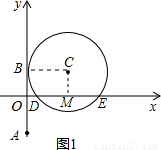
∵OD=1,OE=5,
∴OM=3.
∵OB2=OD•OE=5,
∴OB=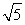 .
.
∴圆心C(3,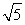 ),半径R=3.
),半径R=3.
(2)∵△POA≌△PHE,
∴PA=PE.
∵OA=OB=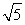 ,OE=5,OP=a,
,OE=5,OP=a,
∴PA2=a2+5,PE2=(5-a)2,
∴a2+5=(a-5)2,
解得:a=2.
(3)过点A作⊙C的切线AT(T为切点),交x轴正半轴于Q.
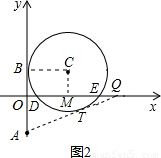
设Q(m,0),则QE=m-5,QD=m-1,
QT=QA-AT=QA-AB=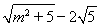 .
.
由QT2=QE•QD,得(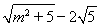 )2=(m-5)(m-1),
)2=(m-5)(m-1),
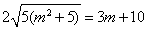
11m2-60m=0.
∵m>0,
∴m=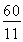 .
.
∵a=6,点P(6,0),在点Q(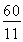 ,0)的右侧,
,0)的右侧,
∴直线AP与⊙C相离.
考点: 1.直线与圆的位置关系;2.直角三角形全等的判定;3.切割线定理.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
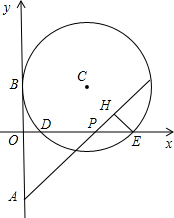 于点B.点A、B关于x轴对称,点P(a,0)在x的正半轴上运动,作直线AP,作EH⊥AP于H.
于点B.点A、B关于x轴对称,点P(a,0)在x的正半轴上运动,作直线AP,作EH⊥AP于H.