��Ŀ����
����Ŀ���Ƽ��ı������ǵ�����������������ѳ�Ϊ���ǵ��ճ���Ҫ��ͨ��ʽ������ϸ���Ҳ�ڷ�������������ı仯��2018����ʡΪ����A��B��������֮��ĸ������У�ij���̿�����ڵ�E����ó���A�ڱ�ƫ��16�������ϣ�����B�ڱ�ƫ��60�������ϣ��ÿ���������������н���7.5km�����F������ʱ��ó���A�ڱ�ƫ��30�������ϣ�����B�ڱ�ƫ��30��������
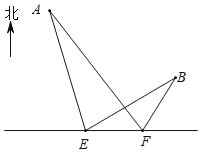
��1��������ѧ��֪ʶ�ж�AB��AE��������ϵ����˵�����ɣ�
��2�������A�ͳ���B֮��ľ���Ϊ���ٹ���������ȷ��1km�����ο����ݣ�![]() ��1.73��cos74���0.28��tan74���3.49��sin76���0.97��cos76���0.24��sin16���0.28��cos16���0.96��
��1.73��cos74���0.28��tan74���3.49��sin76���0.97��cos76���0.24��sin16���0.28��cos16���0.96��
���𰸡�(1) AB��AE,���ɼ���������2������A�ͳ���B֮�����ԼΪ27km��
��������
��1���������������ο��㲢��������ϵ���������ǣ�������ǵ������ҵ���ȵĶ�Ӧ�ǣ����������ѵõ���Ӧ�ߣ�֤��������ȫ�ȣ�
��2������ֱ�������Σ��������Ǻ�����ʾ�漰����ĸ��ߣ������õ�����ϵ�������̲���⼴�ɣ�
�⣺��1��AB��AE
�������£���ͼ
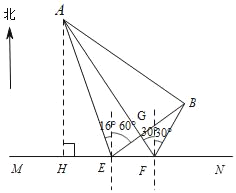
�߳���A�ڵ�E����ƫ��16�������ϣ�����B�ڵ㱱ƫ��60�������ϣ�
���AEH��90����16����74������BEF��90����60����30��
�֡߳���A�ڵ�F��ƫ��30�������ϣ�����B�ڵ�F����ƫ��30�������ϣ�
���AFE��90����30����60������BFN��90����30����60��
���EBF��60����30����30��
��EF��BF
�֡ߡ�BFA��30��+30����60��
����AEF����ABF��
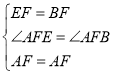
���AEF�ա�ABF��SAS��
��AB��AE
��2����A��AH��MN�ڵ�H��
��AE��x����AH��xsin��90����16������xsin74����HE��xcos��90����16������xcos74��
��HF��xcos74��+7.5
����Rt��AHF��AH��HFtan60��
��xsin74������xcos74��+7.5��tan60��
��0.96x����0.28x+7.5����1.73
���x��27����AB��27
�𣺳���A�ͳ���B֮�����ԼΪ27km��

 һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�
һŵ��ҵ�����ҵ���ּ�����������������ϵ�д�