题目内容
用半径为r的圆形铁皮,做成n个相同圆锥的侧面(不浪费材料,不计接缝处的材料损耗),则每个圆锥的底面半径 .
【答案】分析:易求得圆形铁皮的周长,除以n即为圆锥容器的侧面展开图的弧长,除以2π就是所求的圆锥容器的底面半径.
解答:解:∵半径为r的圆形铁皮,
∴圆形铁皮的周长为2πr,
∴圆锥容器的侧面展开图的弧长为2πr÷n=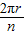 ,
,
∴每个圆锥容器的底面半径为 ÷2π=
÷2π= .
.
故答案为 .
.
点评:本题考查了圆锥的计算,用到的知识点为:圆锥的侧面展开图的弧长等于底面周长.
解答:解:∵半径为r的圆形铁皮,
∴圆形铁皮的周长为2πr,
∴圆锥容器的侧面展开图的弧长为2πr÷n=
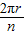 ,
,∴每个圆锥容器的底面半径为
 ÷2π=
÷2π= .
.故答案为
 .
.点评:本题考查了圆锥的计算,用到的知识点为:圆锥的侧面展开图的弧长等于底面周长.

练习册系列答案
相关题目
在半径为50cm的圆形铁皮上剪去一块扇形铁皮,用剩余部分制作成一个底面直径为80cm,母线长为50cm的圆锥形烟囱帽,则剪去的扇形的圆心角度数为( )
| A、228° | B、144° | C、72° | D、36° |
 如图,在一个半径为1cm的圆形铁皮上剪下一个角为60°的阴影BAC,用它围成一个圆锥的侧面,则圆锥的底面圆的半径为
如图,在一个半径为1cm的圆形铁皮上剪下一个角为60°的阴影BAC,用它围成一个圆锥的侧面,则圆锥的底面圆的半径为