题目内容
已知:抛物线 与
与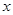 轴的两个交点分别为A、B,点A在点B的左侧,与y轴交于点C,顶点为D,直线
轴的两个交点分别为A、B,点A在点B的左侧,与y轴交于点C,顶点为D,直线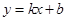 经过点A、C.
经过点A、C.
1.(1)求点D的坐标和直线AC的解析式;
2.(2)点 为抛物线上的一个动点,求使得
为抛物线上的一个动点,求使得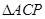 的面积与
的面积与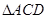 的面积相等的点
的面积相等的点 的坐标.
的坐标.
【答案】
1.(1)由抛物线解析式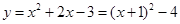 ,
,
得D(-1,-4).--------------------------1分
点A、C的坐标分别是A(-3,0),C(0,-3),
∵直线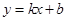 经过A、C两点,
经过A、C两点,
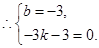
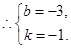
∴ 直线AC的解析式为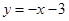 .----------3分
.----------3分
2.(2)①过点D作与直线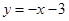 平行的直线,交抛物线于点P.
平行的直线,交抛物线于点P. 
则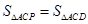 .
.
设直线DP的解析式为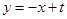 ,
,
∵ 点D的坐标为(-1,-4).∴ t=-5.
∴P(m,-m-5),∴  ,
,
解得 m=-1(舍去)或m=-2.
∴ P(-2,-3). -----------------------------------------------------6分
②直线DP: 与y轴的交点坐标为(0,-5),则直线DP关于直线
与y轴的交点坐标为(0,-5),则直线DP关于直线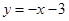 对称的直线
对称的直线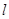 的解析式为
的解析式为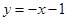 ,
,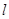 交抛物线于P’,设P’(m’,-m’-1).
交抛物线于P’,设P’(m’,-m’-1).
由于点P’在抛物线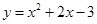 上,∴
上,∴ 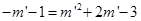 .
.
解得 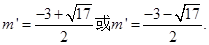 ------------------------------------7分
------------------------------------7分
∴
P’( )或P’(
)或P’(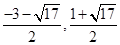 ). --------------8分
). --------------8分
∴ 所求点 的坐标分别是(-2,-3),(
的坐标分别是(-2,-3),( ),(
),(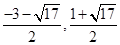 )
)
【解析】略

练习册系列答案
相关题目
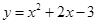 与
与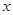 轴的两个交点分别为A、B,点A在点B的左侧,与y轴交于点C,顶点为D,直线
轴的两个交点分别为A、B,点A在点B的左侧,与y轴交于点C,顶点为D,直线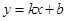 经过点A、C.
经过点A、C.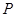 为抛物线上的一个动点,求使得
为抛物线上的一个动点,求使得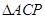 的面积与
的面积与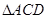 的面积相等的点
的面积相等的点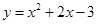 与
与 轴的两个交点分别为A、B,点A在点B的左侧,与y轴交于点C,顶点为D,直线
轴的两个交点分别为A、B,点A在点B的左侧,与y轴交于点C,顶点为D,直线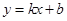 经过点A、C.
经过点A、C.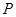 为抛物线上的一个动点,求使得
为抛物线上的一个动点,求使得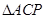 的面积与
的面积与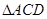 的面积相等的点
的面积相等的点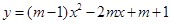 (
( ).
). 轴的交点坐标;
轴的交点坐标; 的值;
的值;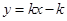 的图象与抛物线始终只有一个公共点,求一次函数的解析式.
的图象与抛物线始终只有一个公共点,求一次函数的解析式.