题目内容
【题目】已知四边形ABCD的四个顶点都在⊙O上，对角线AC和BD交于点E．
（1）若∠BAD和∠BCD的度数之比为1：2，求∠BCD的度数；
（2）若AB＝3，AD＝5，∠BAD＝60°，点C为劣弧BD的中点，求弦AC的长；
（3）若⊙O的半径为1，AC+BD＝3，且AC⊥BD．求线段OE的取值范围．
【答案】（1）120°；（2）
；（3）
≤OE≤
【解析】
(1)利用圆内接四边形对角互补构建方程解决问题即可．
(2)将△ACD绕点C逆时针旋转120°得△CBE，根据旋转的性质得出∠E＝∠CAD＝30°，BE＝AD＝5，AC＝CE，求出A、B、E三点共线，解直角三角形求出即可；
(3)由题知 AC⊥BD，过点O作OM⊥AC于M，ON⊥BD于N，连接OA，OD，判断出四边形OMEN是矩形，进而得出OE2＝2﹣（AC2+BD2），设AC＝m，构建二次函数，利用二次函数的性质解决问题即可．
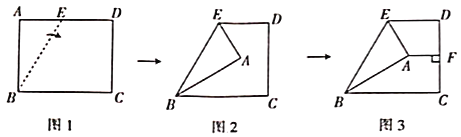
解：(1)如图1中，
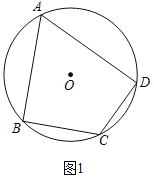
∵四边形ABCD是⊙O的内接四边形，
∴∠A+∠C＝180°，
∵∠A：∠C＝1：2，
∴设∠A＝x，∠C＝2x，则x+2x＝180°，
解得，x＝60°，
∴∠C＝2x＝120°．
(2)如图2中，
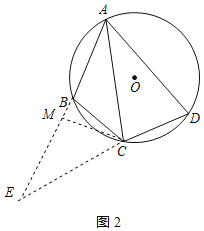
∵A、B、C、D四点共圆，∠BAD＝60°，
∴∠BCD＝180°﹣60°＝120°，
∵点C为弧BD的中点，
∴BC＝CD，∠CAD＝∠CAB＝
∠BAD＝30°，
将△ACD绕点C逆时针旋转120°得△CBE，如图2所示：
则∠E＝∠CAD＝∠CAB＝30°，BE＝AD＝5，AC＝CE，
∴∠ABC+∠EBC＝（180°﹣∠CAB﹣∠ACB）+（180°﹣∠E﹣∠BCE）＝360°﹣（∠CAB+∠ACB+∠ABC）＝360°﹣180°＝180°，
∴A、B、E三点共线，
过C作CM⊥AE于M，
∵AC＝CE，
∴AM＝EM＝AE＝（AB+AD）＝×（3+5）＝4，
在Rt△AMC中，AC＝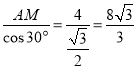
．
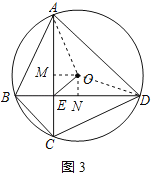
(3) 过点O作OM⊥AC于M，ON⊥BD于N，连接OA，OD，
∵OA＝OD＝1，OM2＝OA2﹣AM2，ON2＝OD2﹣DN2，AM＝AC，DN＝BD，AC⊥BD，
∴四边形OMEN是矩形，
∴ON＝ME，OE2＝OM2+ME2，
∴OE2＝OM2+ON2＝2﹣
（AC2+BD2）
设AC＝m，则BD＝3﹣m，
∵⊙O的半径为1，AC+BD＝3，
∴1≤m≤2，
OE2＝2﹣ [（AC+BD）2﹣2AC×BD]＝﹣m2+
m﹣＝﹣（m﹣）2+
，
∴
≤OE2≤，
∴≤OE≤．
