��Ŀ����
����Ŀ��ij����Ϊ�����ѧ���ۺ����ʣ�������������У���γ̣�A�����鷨��B�����ж���C�ֱʻ���D����������Ϊ���˽�ѧ����ϲ����һ��У���γ̣������ȡ�˲���ѧ�������˵��飬�������������Ƴ���������������ͳ��ͼ����ش��������⣺
��1����α������ѧ�����ж����ˣ�
��2���뽫����ͳ��ͼ��2������������
��3����ƽʱ�Ļ��������Ŀ���ѧϰ�У��ס��ҡ������˱������㣬�־�����������ͬѧ����ѡ�����μ�ȫ���ۺ�����չʾ����ǡ��ͬʱѡ�мס�����λͬѧ�ĸ��ʣ�����״ͼ��������

���𰸡���1��100�ˣ���2����ͼ����������3��![]()
����������1����ϲ�����������������ռ�İٷֱȼ��������������
��2������������ȥϲ��A��B��D���������ϲ��C����������ȫͳ��ͼ���ɣ�
��3�����������г����ó����еȿ��ܵ���������ҳ����������������������������ĸ��ʣ�
�⣺��1����A��36�㣬��Aռ36��360=10%��
��A������Ϊ10�ˣ��� ��α������ѧ�����У�10��10%=100���ˣ���
�� ��α������ѧ����100�ˡ�
��2����ͼ��C�У�100��10��40��20=30���ˣ���
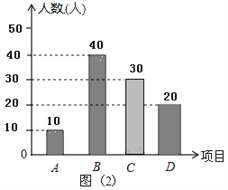
��3������״ͼ�ã�
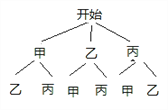
�߹���6�ֵȿ��ܵĽ����ǡ��ͬʱѡ�мס�����λͬѧ����2�������
��ǡ��ͬʱѡ�мס�����λͬѧ�ĸ���Ϊ��![]()
���㾦�����⿼��������ͳ��ͼ������ͳ��ͼ���Լ��б�������״ͼ����Ū�������ǽⱾ��Ĺؼ���

 ����Ӣ��ϵ�д�
����Ӣ��ϵ�д� ����ѧУ�ֲ����ܲ�ϵ�д�
����ѧУ�ֲ����ܲ�ϵ�д� �ƸԺ���ȫ�����Ų��Ծ�ϵ�д�
�ƸԺ���ȫ�����Ų��Ծ�ϵ�д�