题目内容
已知一次函数y=(6+3m)x+n-4.
(1)当m、n为何值时,函数的图象过原点?
(2)当m、n满足什么条件时,函数的图象经过第一、二、三象限?
解:(1)∵一次函数y=(6+3m)x+n-4的图象过原点,
∴6+3m≠0,且n-4=0,
解得,m≠-2,n=4;
(2)∵该函数的图象经过第一、二、三象限,
∴6+3m>0,且n-4>0,
解得m>-2,n>4.
分析:(1)将点(0,0)代入一次函数解析式y=(6+3m)x+n-4求得n值,利用一次函数的性质知系数6+3m≠0求得m值;
(2)根据一次函数的性质知,当该函数的图象经过第一、二、三象限时,6+3m>0,且n-4>0,据此求m、n的值.
点评:本题主要考查一次函数图象在坐标平面内的位置与k、b的关系.解答本题注意理解:直线y=kx+b所在的位置与k、b的符号有直接的关系.k>0时,直线必经过一、三象限.k<0时,直线必经过二、四象限.b>0时,直线与y轴正半轴相交.b=0时,直线过原点;b<0时,直线与y轴负半轴相交.
∴6+3m≠0,且n-4=0,
解得,m≠-2,n=4;
(2)∵该函数的图象经过第一、二、三象限,
∴6+3m>0,且n-4>0,
解得m>-2,n>4.
分析:(1)将点(0,0)代入一次函数解析式y=(6+3m)x+n-4求得n值,利用一次函数的性质知系数6+3m≠0求得m值;
(2)根据一次函数的性质知,当该函数的图象经过第一、二、三象限时,6+3m>0,且n-4>0,据此求m、n的值.
点评:本题主要考查一次函数图象在坐标平面内的位置与k、b的关系.解答本题注意理解:直线y=kx+b所在的位置与k、b的符号有直接的关系.k>0时,直线必经过一、三象限.k<0时,直线必经过二、四象限.b>0时,直线与y轴正半轴相交.b=0时,直线过原点;b<0时,直线与y轴负半轴相交.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
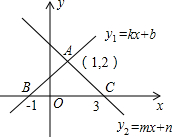 如图所示,已知一次函数y1=kx+b的图象经过A(1,2)、B(-1,0)两点,y2=mx+n的图象经过A、C(3,0)两点,则不等式组0<kx+b<mx+n的解集是( )
如图所示,已知一次函数y1=kx+b的图象经过A(1,2)、B(-1,0)两点,y2=mx+n的图象经过A、C(3,0)两点,则不等式组0<kx+b<mx+n的解集是( )