题目内容
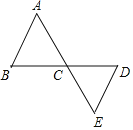
【题目】如图,连接在一起的两个等边三角形的边长都为1cm,一个微型机器人由点A开始按A→B→C→D→E→C→A→B→C…的顺序沿等边三角形的边循环移动.当微型机器人移动了2019cm后,它停在了点_____上.
【答案】D
【解析】
根据等边三角形和全等三角形的性质,可以推出,每行走一圈一共走了6个1cm,2019=6×336+3,行走了336圈又多3cm,即落到D点.
解:∵两个全等的等边三角形的边长为1cm,
∴机器人由A点开始按ABCDBEA的顺序沿等边三角形的边循环运动一圈,即为6cm,
∵2019=6×336+3,即行走了336圈又3cm,
∴行走2016cm后,则这个微型机器人停在A点,再走3cm,则停在D点,
故答案为:D.

练习册系列答案
相关题目