题目内容
若x1，x2，x3的平均数为4，则x1+1，x2+2，x3+3的平均数是 ．
【答案】分析：先根据平均数的定义得到x1+x2+x3=3×4=12，并且x1+1，x2+2，x3+3的平均数=（x1+1+x2+2+x3+3）÷3，然后整体代入进行计算即可．
解答：解：∵x1，x2，x3的平均数为4，
∴x1+x2+x3=3×4=12，
∴x1+1，x2+2，x3+3的平均数为：（x1+1+x2+2+x3+3）÷3=6．
故答案为：6．
点评：本题考查了平均数的计算方法：n个数据x1，x2，…，xn的平均数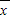
=
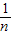（x1+x2+…+xn）．
解答：解：∵x1，x2，x3的平均数为4，
∴x1+x2+x3=3×4=12，
∴x1+1，x2+2，x3+3的平均数为：（x1+1+x2+2+x3+3）÷3=6．
故答案为：6．
点评：本题考查了平均数的计算方法：n个数据x1，x2，…，xn的平均数
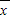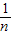=（x1+x2+…+xn）． 
练习册系列答案
相关题目