题目内容
 如图,过⊙O外一点M作⊙O的两条切线,切点为A、B,连接AB、OA、OB、C、D在⊙O上居于弦AB两端,过点D作⊙O的切线交MA、MB于E、F,连接OE、OF、CA、CB,则图中与∠ACB相等的角(不包含∠ACB)有( )
如图,过⊙O外一点M作⊙O的两条切线,切点为A、B,连接AB、OA、OB、C、D在⊙O上居于弦AB两端,过点D作⊙O的切线交MA、MB于E、F,连接OE、OF、CA、CB,则图中与∠ACB相等的角(不包含∠ACB)有( )分析:由过⊙O外一点M作⊙O的两条切线,切点为A、B,易得∠AOM=∠BOM=
∠AOB,又由∠ACB=
∠AOB,即可得∠AOM=∠BOM=∠ACB,然后由连接OD,OD是⊙O的切线,同理可得:∠AOE=∠DOE,∠BOF=∠DOF,即可得∠EOF=
∠AOB,则可得∠EOF=∠ACB.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答: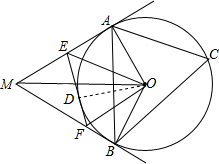 解:∵过⊙O外一点M作⊙O的两条切线,切点为A、B,
解:∵过⊙O外一点M作⊙O的两条切线,切点为A、B,
∴∠AMO=∠BMO,OA⊥AM,OB⊥BM,
∴∠AOM=∠BOM=
∠AOB,
∵∠ACB=
∠AOB,
∴∠AOM=∠BOM=∠ACB;
连接OD,
∵OD是⊙O的切线,
同理可得:∠AOE=∠DOE,∠BOF=∠DOF,
∴∠EOF=∠EOD+∠DOF=
∠AOB,
∴∠EOF=∠ACB;
∴图中与∠ACB相等的角(不包含∠ACB)有3个.
故选A.
 解:∵过⊙O外一点M作⊙O的两条切线,切点为A、B,
解:∵过⊙O外一点M作⊙O的两条切线,切点为A、B,∴∠AMO=∠BMO,OA⊥AM,OB⊥BM,
∴∠AOM=∠BOM=
| 1 |
| 2 |
∵∠ACB=
| 1 |
| 2 |
∴∠AOM=∠BOM=∠ACB;
连接OD,
∵OD是⊙O的切线,
同理可得:∠AOE=∠DOE,∠BOF=∠DOF,
∴∠EOF=∠EOD+∠DOF=
| 1 |
| 2 |
∴∠EOF=∠ACB;
∴图中与∠ACB相等的角(不包含∠ACB)有3个.
故选A.
点评:此题考查了切线的性质以及圆周角定理.此题难度适中,注意掌握辅助线的作法,注意掌握数形结合思想的应用.

练习册系列答案
相关题目
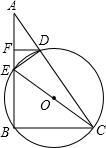 如图,过⊙O外一点A向⊙O引割线AEB,ADC,DF∥BC,交AB于F.若CE过圆心O,D是AC中点.
如图,过⊙O外一点A向⊙O引割线AEB,ADC,DF∥BC,交AB于F.若CE过圆心O,D是AC中点.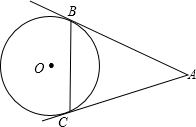 如图,过⊙O外一点A引切线AB、AC,B、C为切点,若∠BAC=60°,BC=8cm,则⊙O的直径是
如图,过⊙O外一点A引切线AB、AC,B、C为切点,若∠BAC=60°,BC=8cm,则⊙O的直径是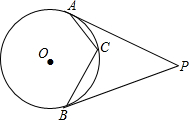 如图,过⊙O外一点P作两条切线,切点分别为A、B,C为劣弧AB上一点,若∠ACB=122°,则∠APB=
如图,过⊙O外一点P作两条切线,切点分别为A、B,C为劣弧AB上一点,若∠ACB=122°,则∠APB= (2012•安庆一模)如图,过⊙O外一点P作⊙O的两条切线PA、PB,切点分别为A、B.下列结论中,正确的是
(2012•安庆一模)如图,过⊙O外一点P作⊙O的两条切线PA、PB,切点分别为A、B.下列结论中,正确的是