题目内容
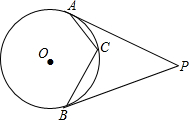 如图,过⊙O外一点P作两条切线,切点分别为A、B,C为劣弧AB上一点,若∠ACB=122°,则∠APB=
如图,过⊙O外一点P作两条切线,切点分别为A、B,C为劣弧AB上一点,若∠ACB=122°,则∠APB=64°
64°
.分析:连接OA,OB,作圆周角∠AEB,根据切线的性质得出∠PAO=∠PBO=90°,根据圆内接四边形性质得出∠AEB+∠ACB=180°,求出∠AEB=58°,根据圆周角定理得出∠AOB=2∠AEB=116°,根据多边形内角和定理求出即可.
解答:解:
连接OA,OB,如图作圆周角∠AEB,
∵过⊙O外一点P作两条切线,切点分别为A、B,
∴∠PAO=∠PBO=90°,
∵∠ACB=122°,E、A、C、B四点共圆,
∴∠AEB+∠ACB=180°,
∴∠AEB=58°,
∴有圆周角定理得:∠AOB=2∠AEB=116°,
∴∠APB=360°-∠PAO-∠PBO-∠AOB=360°-90°-90°-116°=64°,
故答案为:64°.

连接OA,OB,如图作圆周角∠AEB,
∵过⊙O外一点P作两条切线,切点分别为A、B,
∴∠PAO=∠PBO=90°,
∵∠ACB=122°,E、A、C、B四点共圆,
∴∠AEB+∠ACB=180°,
∴∠AEB=58°,
∴有圆周角定理得:∠AOB=2∠AEB=116°,
∴∠APB=360°-∠PAO-∠PBO-∠AOB=360°-90°-90°-116°=64°,
故答案为:64°.
点评:本题考查了切线的性质,圆内接四边形性质,圆周角定理,多边形内角和定理的应用,主要考查学生的推理能力.

练习册系列答案
 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
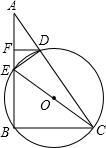 如图,过⊙O外一点A向⊙O引割线AEB,ADC,DF∥BC,交AB于F.若CE过圆心O,D是AC中点.
如图,过⊙O外一点A向⊙O引割线AEB,ADC,DF∥BC,交AB于F.若CE过圆心O,D是AC中点.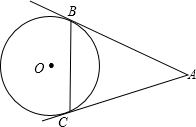 如图,过⊙O外一点A引切线AB、AC,B、C为切点,若∠BAC=60°,BC=8cm,则⊙O的直径是
如图,过⊙O外一点A引切线AB、AC,B、C为切点,若∠BAC=60°,BC=8cm,则⊙O的直径是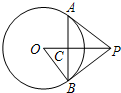 (2012•安庆一模)如图,过⊙O外一点P作⊙O的两条切线PA、PB,切点分别为A、B.下列结论中,正确的是
(2012•安庆一模)如图,过⊙O外一点P作⊙O的两条切线PA、PB,切点分别为A、B.下列结论中,正确的是 如图,过⊙O外一点M作⊙O的两条切线,切点为A、B,连接AB、OA、OB、C、D在⊙O上居于弦AB两端,过点D作⊙O的切线交MA、MB于E、F,连接OE、OF、CA、CB,则图中与∠ACB相等的角(不包含∠ACB)有( )
如图,过⊙O外一点M作⊙O的两条切线,切点为A、B,连接AB、OA、OB、C、D在⊙O上居于弦AB两端,过点D作⊙O的切线交MA、MB于E、F,连接OE、OF、CA、CB,则图中与∠ACB相等的角(不包含∠ACB)有( )