题目内容
(2006•大连)如图,抛物线E:y=x2+4x+3交x轴于A、B两点,交y轴于M点,抛物线E关于y轴对称的抛物线F交x轴于C、D两点.(1)求F的解析式;
(2)在x轴上方的抛物线F或E上是否存在一点N,使以A、C、N、M为顶点的四边形是平行四边形?若存在,求点N的坐标;若不存在,请说明理由;
(3)若将抛物线E的解析式改为y=ax2+bx+c,试探索问题(2).

【答案】分析:(1)令y=0,可求出抛物线E与x轴的两个交点坐标,再令x=0,可求出与y轴的交点M,可以得到这三点关于y轴对称的点,设抛物线F的解析式是y=ax2+bx+3,直接把AB的对称点的坐标代入F的解析式,即可求出F的解析式.
(2)若使以A、C、N、M为顶点的四边形是平行四边形,那么应有MN∥AC,即N,M两点的纵坐标相同,可将M点的总坐标代入两抛物线的解析式中求出N点的坐标,然后看MN是否与AC的长相等即可判断出是否存在符合条件的N点.
(3)同(2)一样,也要先用代数式表示出A、C、M的坐标,然后用M的纵坐标求出N点的坐标,进而去比较MN和AC的长是否相等.
解答: 解:(1)解法一:当y=0时,x2+4x+3=0,
解:(1)解法一:当y=0时,x2+4x+3=0,
解得x1=-3,x2=-1,
∴A、B点坐标分别为(-3,0)、(-1,0);
当x=0时,y=3,
∴M点坐标为(0,3),A、B、M三点关于y轴得对称点分别是D、C、M,
∴D、C坐标为(3,0)、(1,0);
设F的解析式为y=ax2+bx+3,则有: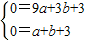 ,
,
∴a=1,b=-4
∴抛物线F的解析式为y=x2-4x+3.
解法二:∵抛物线E与抛物线F关于y轴对称,且抛物线E:y=x2+4x+3,
∴抛物线F的方程是:y=(-x)2+4×(-x)+3=x2-4x+3,即
抛物线F的解析式为y=x2-4x+3;
(2)存在.假设MN∥AC,
∴N点的纵坐标为3.
若在抛物线F上,当y=3时,3=x2-4x+3,则x1=0,x2=4
∴N点坐标为(4,3),
∴MN=4,
由(1)可求AC=4,
∴MN=AC,
∴四边形ACNM为平行四边形.
根据抛物线F和E关于y轴对称,故N点坐标为(4,3)或(-4,3).
(3)存在.假设MN∥AC,
∴N点的纵坐标为c.设y=0,
∴ax2+bx+c=0
∴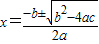 ,
,
∴A点坐标为(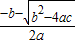 ,0),
,0),
B点坐标为(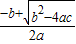 ,0)
,0)
∴C点坐标为(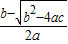 ,0),
,0),
∴AC=
在抛物线E上,当y=c时,c=ax2+bx+c,x1=0,x2=
∴N点坐标为( ,c)
,c)
NM=0-( )=
)= ,
,
∴NM=AC,
∴四边形ACMN为平行四边形.
根据抛物线F和E关于y轴对称,故N点坐标为( ,c)或(
,c)或(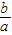 ,c).
,c).
点评:本题主要考查了二次函数解析式的确定,轴对称图形,平行四边形的判定等知识点.
(2)若使以A、C、N、M为顶点的四边形是平行四边形,那么应有MN∥AC,即N,M两点的纵坐标相同,可将M点的总坐标代入两抛物线的解析式中求出N点的坐标,然后看MN是否与AC的长相等即可判断出是否存在符合条件的N点.
(3)同(2)一样,也要先用代数式表示出A、C、M的坐标,然后用M的纵坐标求出N点的坐标,进而去比较MN和AC的长是否相等.
解答:
 解:(1)解法一:当y=0时,x2+4x+3=0,
解:(1)解法一:当y=0时,x2+4x+3=0,解得x1=-3,x2=-1,
∴A、B点坐标分别为(-3,0)、(-1,0);
当x=0时,y=3,
∴M点坐标为(0,3),A、B、M三点关于y轴得对称点分别是D、C、M,
∴D、C坐标为(3,0)、(1,0);
设F的解析式为y=ax2+bx+3,则有:
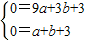 ,
,∴a=1,b=-4
∴抛物线F的解析式为y=x2-4x+3.
解法二:∵抛物线E与抛物线F关于y轴对称,且抛物线E:y=x2+4x+3,
∴抛物线F的方程是:y=(-x)2+4×(-x)+3=x2-4x+3,即
抛物线F的解析式为y=x2-4x+3;
(2)存在.假设MN∥AC,
∴N点的纵坐标为3.
若在抛物线F上,当y=3时,3=x2-4x+3,则x1=0,x2=4
∴N点坐标为(4,3),
∴MN=4,
由(1)可求AC=4,
∴MN=AC,
∴四边形ACNM为平行四边形.
根据抛物线F和E关于y轴对称,故N点坐标为(4,3)或(-4,3).
(3)存在.假设MN∥AC,
∴N点的纵坐标为c.设y=0,
∴ax2+bx+c=0
∴
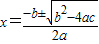 ,
,∴A点坐标为(
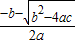 ,0),
,0),B点坐标为(
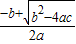 ,0)
,0)∴C点坐标为(
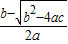 ,0),
,0),∴AC=

在抛物线E上,当y=c时,c=ax2+bx+c,x1=0,x2=

∴N点坐标为(
 ,c)
,c)NM=0-(
 )=
)= ,
,∴NM=AC,
∴四边形ACMN为平行四边形.
根据抛物线F和E关于y轴对称,故N点坐标为(
 ,c)或(
,c)或(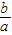 ,c).
,c).点评:本题主要考查了二次函数解析式的确定,轴对称图形,平行四边形的判定等知识点.

练习册系列答案
相关题目