��Ŀ����
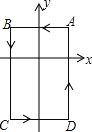
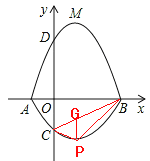
����Ŀ����ͼ����ƽ��ֱ������ϵ![]() �У�A��BΪx�������㣬C��DΪy���ϵ����㣬������A��C��B�������ߵ�һ����C1�뾭����A��D��B�������ߵ�һ����C2��ϳ�һ��������ߣ����ǰ�����������߳�Ϊ�����ߡ�����֪��C������Ϊ��0��
�У�A��BΪx�������㣬C��DΪy���ϵ����㣬������A��C��B�������ߵ�һ����C1�뾭����A��D��B�������ߵ�һ����C2��ϳ�һ��������ߣ����ǰ�����������߳�Ϊ�����ߡ�����֪��C������Ϊ��0��![]() ������M��������C2��
������M��������C2��![]() ��
��![]() ��0���Ķ��㣮
��0���Ķ��㣮
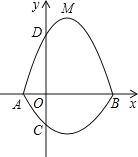
��1����A��B��������ꣻ
��2������BDMΪֱ��������ʱ����![]() ��ֵ��
��ֵ��
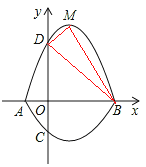
��3�������ߡ��ڵ����������Ƿ����һ��P��ʹ����PBC�������������ڣ������PBC��������ֵ���������ڣ���˵�����ɣ�
���𰸡���1��A��-1��0����B��3��0������2��-![]() ;��3��P��
;��3��P��![]() ��-
��-![]() ����
����![]() .
.
��������
�������: ��1����y=mx2-2mx-3m��Ϊ����ʽ�����ɵõ�A��B��������ꣻ
��2���ȱ�ʾ��DM2��BD2��MB2��������DM2+MB2=BD2���������m��ֵ��
��3�����ô���ϵ�����õ�������C1�Ľ���ʽ������P��PQ��y�ᣬ��BC��Q���ô���ϵ�����õ�ֱ��BC�Ľ���ʽ���ٸ��������ε������ʽ���䷽���õ���PBC��������ֵ��
�����������1��������ɵã�y=mx2-2mx-3m=m��x-3����x+1����
��m��0��
����y=0ʱ��0=m��x-3����x+1����
��ã�x1=-1��x2=3��
��A��-1��0����B��3��0����
��2����ͼ1��
��y=mx2-2mx-3m=m��x-1��2-4m��
������M���꣨1��-4m����
��x=0ʱ��y=-3m��
��D��0��-3m����B��3��0����
��DM2=��0-1��2+��-3m+4m��2=m2+1��
MB2=��3-1��2+��0+4m��2=16m2+4��
BD2=��3-0��2+��0+3m��2=9m2+9��
����BDMΪRt������MΪֱ�ǵ�ֱ��������ʱ���У�DM2+MB2=BD2��
DM2+MB2=BD2ʱ�У�m2+1+16m2+4=9m2+9��
���m=-![]() ��m=
��m=![]() ��ȥ����
��ȥ����
��m=-![]() ʱ����BDMΪ����MΪֱ�ǵ�ֱ�������Σ�
ʱ����BDMΪ����MΪֱ�ǵ�ֱ�������Σ�
��3����C1��y=ax2+bx+c����A��B��C������������ã�
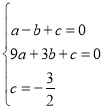 �� ���
�� ��� ��
��
��C1��y=![]() x2-x-
x2-x-![]() ��
��
��ͼ2������P��PQ��y�ᣬ��BC��Q��
��B��C������ɵ�ֱ��BC�Ľ���ʽΪ��y=![]() x-
x-![]() ��
��
��P��x��![]() x2-x-
x2-x-![]() ������Q��x��
������Q��x��![]() x-
x-![]() ����
����
PQ=![]() x-
x-![]() -��
-��![]() x2-x-
x2-x-![]() ��=-
��=-![]() x2+
x2+![]() x��
x��
S��PBC=S��PCQ+S��PBQ=![]() PQ
PQ![]() OB=
OB=![]() ����-
����-![]() x2+
x2+![]() x����3=-
x����3=-![]() ��x-
��x-![]() ��2+
��2+![]() ��
��
��x=![]() ʱ��S��PBC�����ֵ��Smax=
ʱ��S��PBC�����ֵ��Smax=![]() ��
��
��![]() ����
����![]() ��2-
��2-![]() -
-![]() =-
=-![]() ��
��
��P��![]() ��-
��-![]() ����
����

 һ������ϵ�д�
һ������ϵ�д� �Ƹ�С״Ԫ���ֳ������ϵ�д�
�Ƹ�С״Ԫ���ֳ������ϵ�д� �¸��̵�ѧϵ�д�
�¸��̵�ѧϵ�д� ����ͬѧһ����ʦȫ�źþ�ϵ�д�
����ͬѧһ����ʦȫ�źþ�ϵ�д�